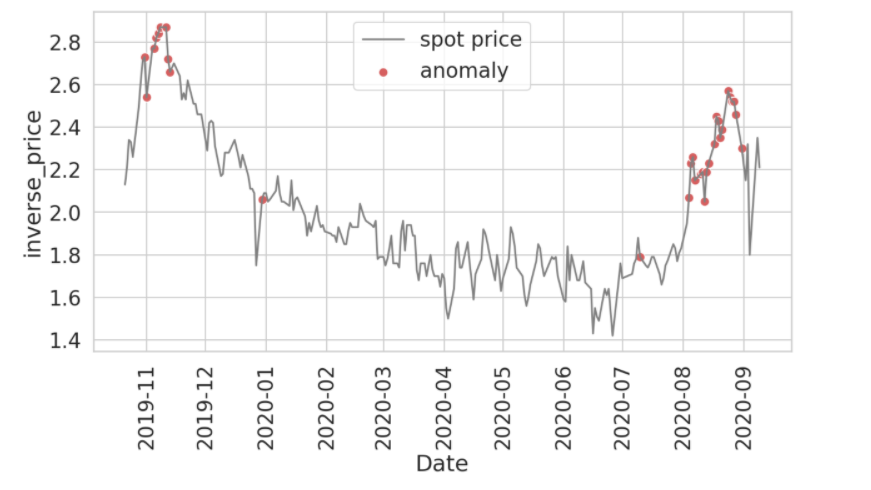
실제 결과는 가격 예측에서 예측된 결과와 다릅니다. 우리가 알고 있듯이 실제 데이터는 스트리밍, 시계열 데이터 등이 있으며, 여기서 변칙성은 중요한 상황에서 중요한 정보를 제공합니다. 이상 감지에서 우리는 비정상적이거나 비정상적이거나 예상치 못한 기록을 발견하는 데 관심이 있으며 시계열 컨텍스트에서 이상은 단일 레코드의 범위 내에서 또는 하위 시퀀스/패턴으로 감지될 수 있습니다.
과거 데이터를 추정하는 시계열 기반 예측 모델은 현재 데이터로 추정하여 미래 가격을 예측하는 데 도움이 됩니다. 일단 예측을 하면 해당 데이터를 사용하여 실제와 비교할 때 이상을 감지할 수 있습니다.
그것을 구현하고 장단점을 살펴 보겠습니다. 따라서 여기에서 우리의 목표는 시계열 데이터에 대한 이상 감지 모델을 개발하는 것입니다. 이 사용 사례에서는 신경망 아키텍처를 사용할 것입니다.
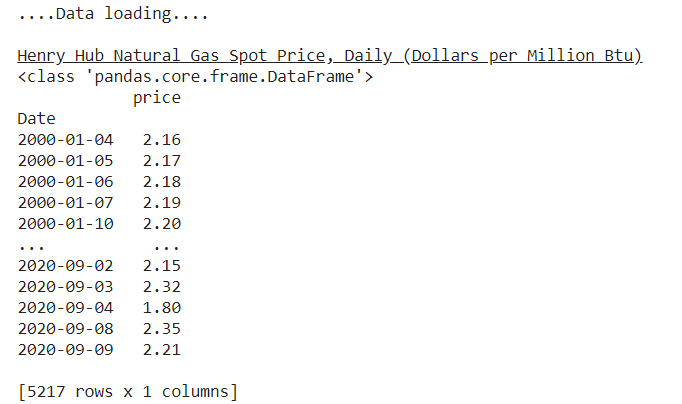
EIA에서 Henry Hub Spot Price 데이터를 로드해 보겠습니다. 여기서 데이터의 순서는 중요하며 다음 시점을 예측할 때 시간순이어야 함을 기억해야 합니다.
print("....Data loading....")
print() # Henry Hub Spot Price, Daily
print('\033[4mHenry Hub Natural Gas Spot Price, Daily (Dollars per Million Btu)\033[0m')
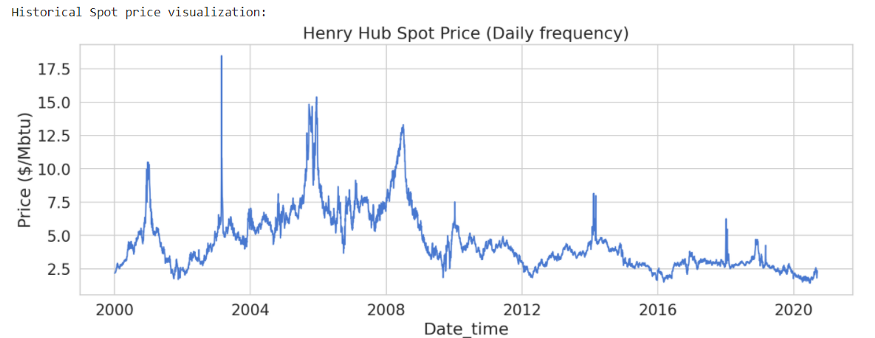
Raw 데이터 시각화:
print('Historical Spot price visualization:')
plt.figure(figsize = (15,5))
plt.plot(spot_price)
plt.title('Henry Hub Spot Price (Daily frequency)')
plt.xlabel ('Date_time')
plt.ylabel ('Price ($/Mbtu)')
plt.show()
print('Missing values:', spot_price.isnull().sum())
# checking missing values
spot_price = spot_price.dropna()
# dropping missing valies
print('....Dropped Missing value row....')
print('Rechecking Missing values:', spot_price.isnull().sum())
# checking missing values

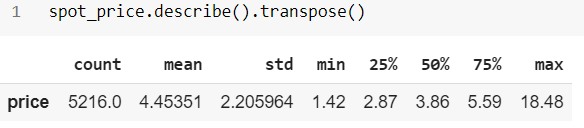
다양한 시장 조작 유형의 공통적인 특징은 데이터의 예상치 못한 패턴이나 행동입니다.
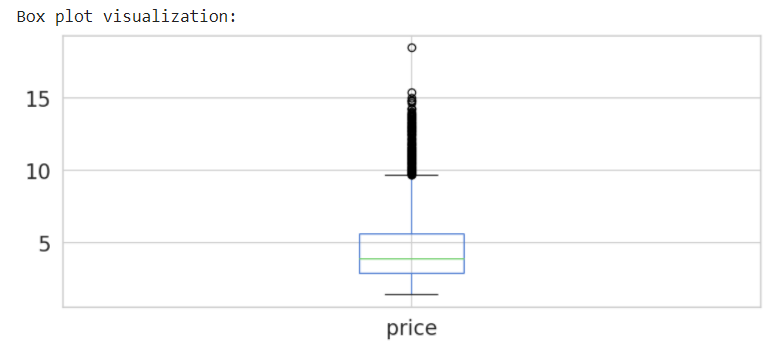
# Generate Boxplot
print('Box plot visualization:')
spot_price.plot(kind='box', figsize = (10,4))
plt.show()
# Generate Histogram
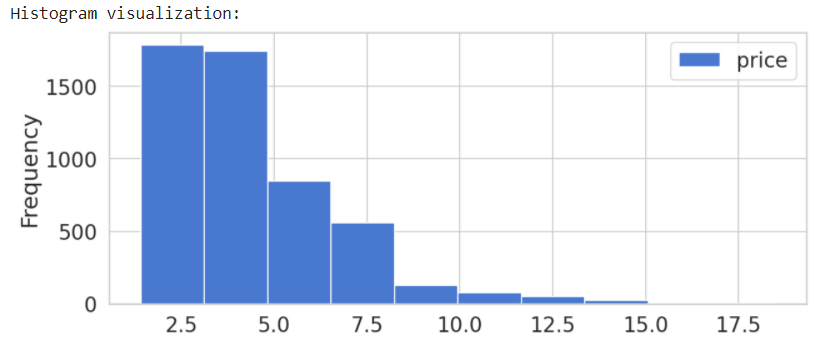
print('Histogram visualization:')
spot_price.plot(kind='hist', figsize = (10,4) )
plt.show()
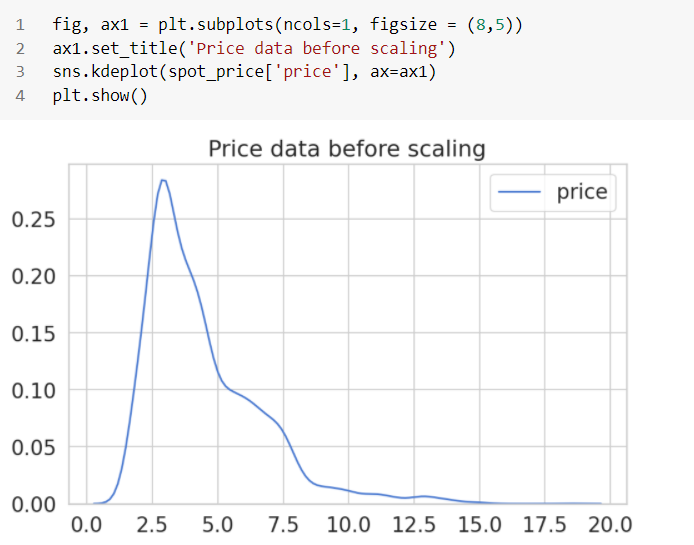
변칙적인 하위 시퀀스 감지:
여기서 목표는 주어진 긴 시계열(시퀀스) 내에서 변칙적인 부분 시퀀스를 식별하는 것입니다.
이상 탐지는 정상이 아닌 것을 발견하기 위해 정상을 모델링하는 기본 개념을 기반으로 합니다....Dunning & Friedman
전처리:
데이터의 95%를 사용하고 이를 기반으로 모델을 훈련합니다.
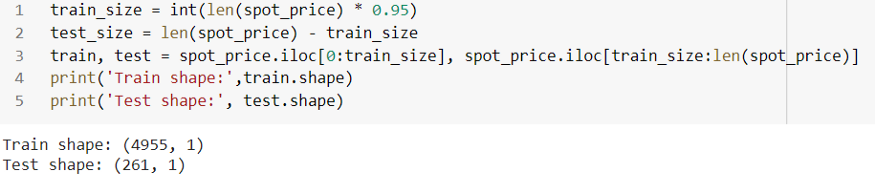
다음으로 훈련 데이터를 사용하여 데이터를 확장하고 동일한 변환을 테스트 데이터에 적용합니다. 나는 아래와 같이 Robust scaler를 사용했습니다.
# data standardization
robust = RobustScaler(quantile_range=(25, 75)).fit(train[['price']])
train['price'] = robust.transform(train[['price']])
test['price'] = robust.transform(test[['price']])
마지막으로 도우미 함수를 사용하여 데이터를 하위 시퀀스로 분할합니다.
# helper function
def create_dataset(X, y, time_steps=1):
a, b = [], []
for i in range(len(X) - time_steps):
v = X.iloc[i:(i + time_steps)].values
a.append(v)
b.append(y.iloc[i + time_steps])
return np.array(a), np.array(b)
# We’ll create sequences with 30 days of historical data
n_steps = 30
# reshape to 3D [n_samples, n_steps, n_features]
X_train, y_train = create_dataset(train[['price']], train['price'], n_steps)
X_test, y_test = create_dataset(test[['price']], test['price'], n_steps)
print('X_train shape:', X_train.shape)
print('X_test shape:', X_test.shape)
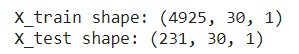
Keras의 LSTM AE:
Autoencoder는 입력의 압축된 표현을 개발하기 위해 데이터 내의 구조를 발견할 수 있는 신경망 아키텍처의 것입니다. 입력 시퀀스를 숨겨진 표현으로 읽는 인코더로 순환 네트워크를 사용합니다. 그런 다음, 표현은 디코더 순환 네트워크에 공급되어 입력 시퀀스 자체를 재구성합니다.
여기에서 Autoencoder는 시퀀스를 입력으로 취하고 동일한 모양의 시퀀스를 출력해야 합니다. 시퀀스에 총 5219개의 데이터 포인트가 있으며 우리의 목표는 이상을 찾는 것입니다. 데이터 포인트가 비정상인 경우를 찾으려고 합니다.
't-1' 까지의 과거 데이터를 기반으로 시간 't' 의 데이터 포인트를 예측할 수 있다면 실제 값과 비교하여 예상 값을 보고 예상 범위 내에 있는지 확인할 수 있습니다. 시간 't'에 대한 값.
y_pred 를 실제 값( y_test )과 비교할 수 있습니다 . y_pred 와 y_test 의 차이 는 오류를 제공하고 시퀀스의 모든 점에 대한 오류를 얻으면 오류의 분포만 남게 됩니다. 이를 수행하기 위해 Keras를 사용하는 순차 모델을 사용합니다.
모델 아키텍처:
- 모델은 LSTM 레이어와 고밀도 레이어로 구성됩니다.
- LSTM 계층은 시계열 데이터를 입력으로 받아 시간에 대한 값을 학습하는 방법을 학습합니다.
- 다음 레이어는 조밀한 레이어(완전 연결 레이어)입니다.
- 조밀한 계층은 LSTM 계층의 출력을 입력으로 받아 완전히 연결된 방식으로 변환합니다.
- 그런 다음 최종 출력이 0과 1 사이가 되도록 조밀한 계층에 시그모이드 활성화를 적용합니다.
우리는 또한 'adam' 옵티마이저와 '평균 제곱 오차'를 손실 함수로 사용합니다.
시퀀스 문제:
- ML 알고리즘 및 신경망은 고정 길이 입력으로 작동하도록 설계되었습니다.
- 관찰의 시간적 순서는 지도 학습 모델에 대한 입력으로 사용하기에 적합한 특징을 추출하는 것을 어렵게 만들 수 있습니다.

# history for loss
plt.figure(figsize = (10,5))
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
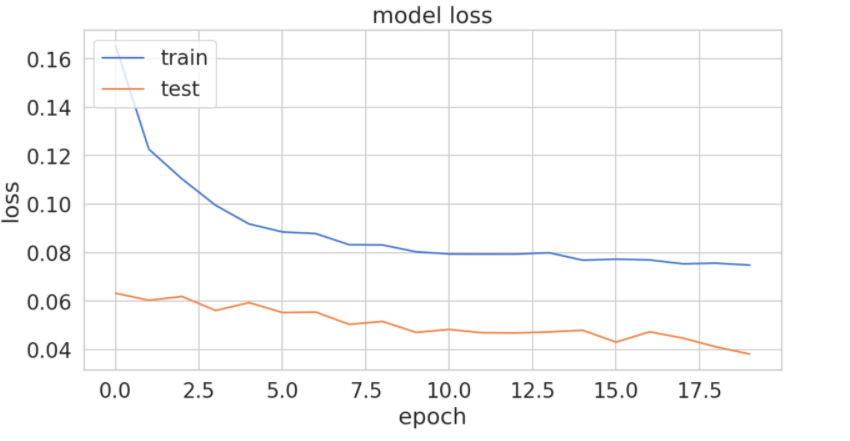
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='upper left')
plt.show()
평가:
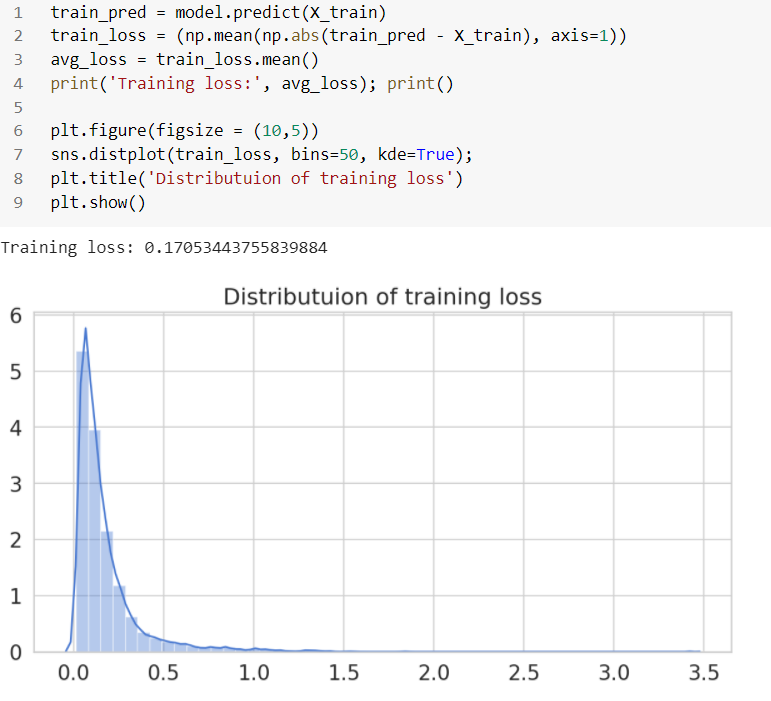
모델이 훈련되면 테스트 데이터 세트를 사용하여 예측하고 오류(mae)를 계산할 수 있습니다. 훈련 데이터에서 MAE(평균 절대 오차)를 계산하는 것부터 시작하겠습니다.
테스트 데이터의 정확도 측정항목:
# MAE on the test data:
y_pred = model.predict(X_test)
print('Predict shape:', y_pred.shape); print();
mae = np.mean(np.abs(y_pred - X_test), axis=1)
# reshaping prediction
pred = y_pred.reshape((y_pred.shape[0] * y_pred.shape[1]), y_pred.shape[2])
print('Prediction:', pred.shape); print();
print('Test data shape:', X_test.shape); print();
# reshaping test data
X_test = X_test.reshape((X_test.shape[0] * X_test.shape[1]), X_test.shape[2])
print('Test data:', X_test.shape); print();
# error computation
errors = X_test - pred
print('Error:', errors.shape); print();
# rmse on test data
RMSE = math.sqrt(mean_squared_error(X_test, pred_reshape))
print('Test RMSE: %.3f' % RMSE);

RMSE는 0.099로 낮으며, 이는 20 Epochs: loss: 0.0749 - val_loss: 0.0382 후 학습 단계의 낮은 손실에서도 분명합니다. 이것은 오류가 낮지만 실제의 변칙적 행동을 이것을 사용하여 식별할 수 없는 좋은 예측일 수 있지만.
임계값 계산:

목표는 오류가 선택한 임계값보다 클 때 이상을 감지하는 것입니다.

우리가 극단값을 아주 잘 임계화하고 있는 것 같습니다. 다음 항목만 사용하여 데이터 프레임을 생성해 보겠습니다.
이상 보고서 형식:
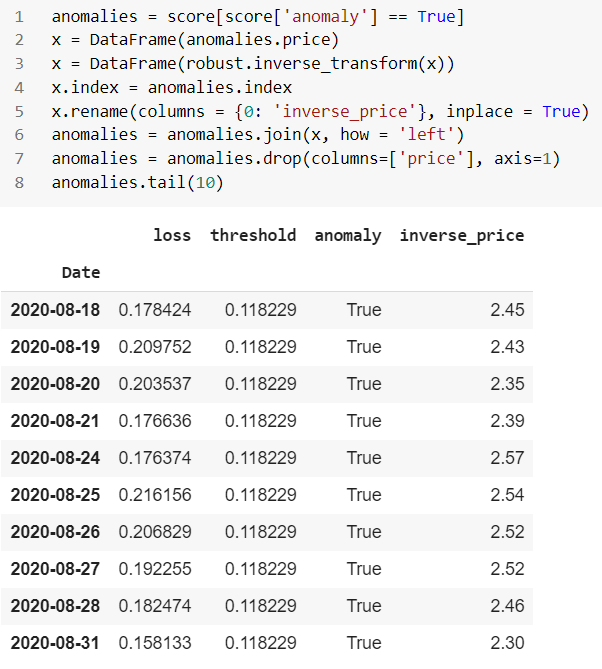
역 테스트 데이터:
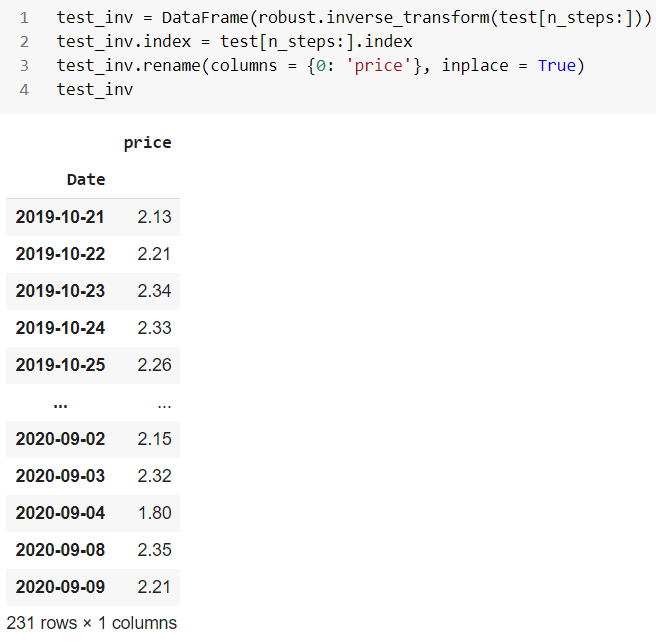
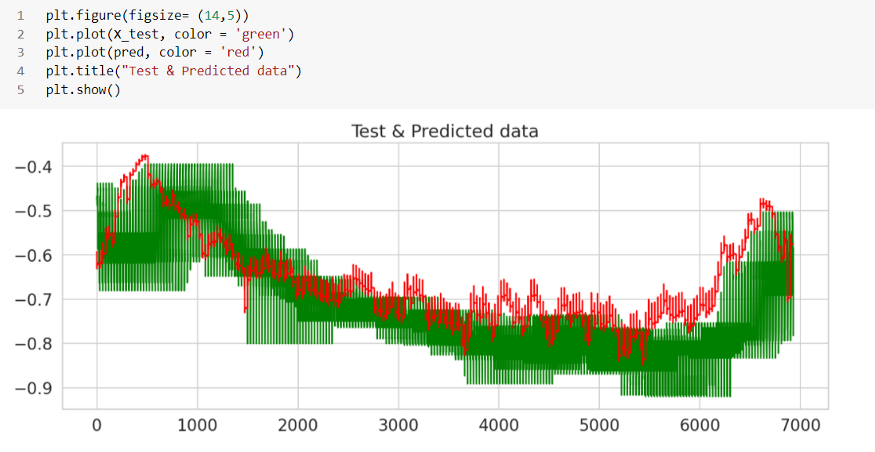
마지막으로 테스트 데이터에서 발견된 이상 현상을 살펴보겠습니다.
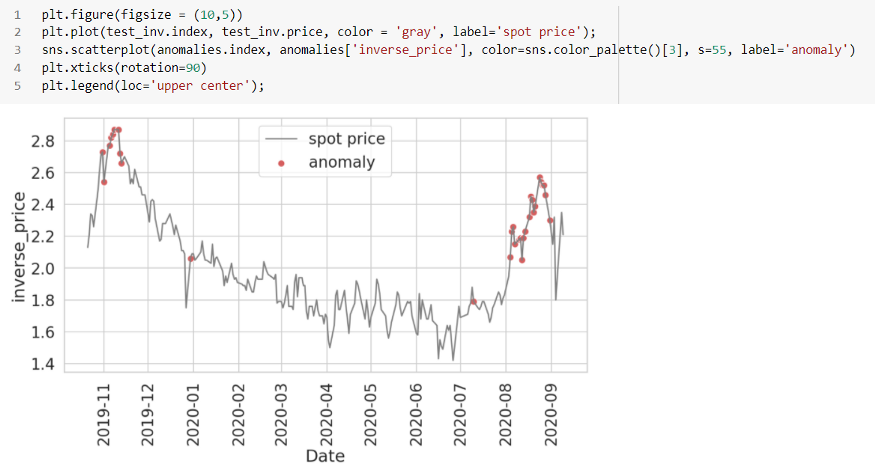
빨간 점은 여기의 이상 현상으로 기존 현물 가격의 급격한 변화로 대부분의 포인트를 덮고 있습니다. 임계값은 우리가 선택한 매개변수, 특히 컷오프 값에 따라 변경할 수 있습니다. 시간 단계 수, 임계값 컷오프, 신경망의 에포크, 배치 크기, 은닉층 등과 같이 사용한 매개변수 중 일부를 가지고 놀면 다른 결과 세트를 기대할 수 있습니다.
이것으로 우리는 주식 거래와 관련하여 시계열에서 이상 현상을 찾는 것에 대한 간략한 프로젝트를 마칩니다.
'Daily Review' 카테고리의 다른 글
| 데이터사이언티스트에게 필요한 3가지 이상 탐지 모델(Anomaly Detection) (0) | 2022.09.01 |
|---|---|
| Data-Driven Organization을 향한 디자인 씽킹 (0) | 2022.09.01 |
| Autoencoder를 활용한 이미지 이상 탐지 (0) | 2022.08.31 |
| 데이터 사이언티스트가 꼭 알아야 하는 '통계적 가설 검증법' 1가지. (0) | 2022.08.31 |
| 스파게티 차트(Spaghetti Charts) 대신 제안된 대안: 격자 차트(Trellis Chart) (0) | 2022.08.31 |




댓글