
Wikipedia는 총 104개의 통계 테스트 를 집계합니다.
데이터 과학자는 압도당하고 스스로에게 다음과 같이 질문할 수 있습니다.
“내가 다 알아야 합니까? 그리고 언제 다른 것을 사용해야 하는지 어떻게 알 수 있습니까?”
데이터 전문가로서 여러분이 알아야 할 테스트는 단 하나입니다.
하나의 테스트는 중요하고 다른 103개의 테스트는 무시할 수 있기 때문이 아닙니다.
하지만 다음과 같은 이유로: 모든 통계 테스트는 실제로 동일한 하나의 테스트입니다!
그리고 일단 이 테스트가 어떻게 작동하는지 진정으로 이해하면, 당신은 당신이 필요로 하는 어떤 가설도 테스트할 수 있을 것입니다.
증거를 원하십니까? 이 기사에서는 4가지 매우 다양한 통계 문제를 해결할 것입니다. 그리고 우리는 항상 동일한 정확한 알고리즘을 사용하여 문제를 해결할 것입니다.
- 주사위를 10번 던졌습니다. 당신은 [1, 1, 1, 1, 1, 2, 2, 2, 3, 3]을 얻었습니다. 주사위가 장전되었습니까?
- 당신의 친구는 가방에서 일부 스크래블 타일이 떨어졌고 우연히 그 글자가 "FEAR"라는 실제 단어를 형성했다고 주장합니다. 당신은 당신의 친구가 당신을 놀리려는 것 같다고 생각합니다. 친구가 거짓말을 하고 있나요?
- 고객 만족도 조사에서 100명의 고객이 제품 A에 3.00, 제품 B에 2.63의 평균 평점을 주었습니다. 이 차이가 중요합니까?
- 이진 분류 모델을 학습했습니다. 테스트 세트(100개의 관찰으로 구성)에서 ROC 곡선 아래 영역이 70%입니다. 모델이 무작위보다 훨씬 더 나은가요?
이러한 질문에 대한 답을 알아보기 전에 통계적 테스트가 무엇인지에 대해 알아보도록 하겠습니다.
통계 테스트의 심오한 의미는 무엇입니까?
나는 통계에서 가장 독창적이지 않은 예인 주사위 던지기로 이 질문에 답하려고 노력할 것입니다.
주사위를 여섯 번 던졌고 [2, 2, 2, 2, 2, 4]가 나왔다고 상상해 보십시오. 좀 의심스럽죠? 당신은 6번 중 5번과 같은 숫자를 기대하지 않습니다. 적어도 주사위가 공정하다면 그런 일이 일어날 것이라고 기대하지 않습니다 .
이것이 바로 통계 테스트의 핵심입니다.
"귀무 가설"이라고 하는 가설이 있고 이를 테스트하려고 합니다. 따라서 다음과 같이 자문합니다.
"가설이 사실이라면 얼마나 자주 내가 실제로 얻은 결과만큼 의심스러운 결과를 얻을 수 있습니까?"
주사위의 예에서 질문은 다음과 같습니다. "주사가 공정한 경우 [2, 2, 2, 2, 2, 4]와 같은 예기치 않은 시퀀스가 얼마나 자주 나올까요?" "얼마나 자주"를 묻는 것이므로 대답은 반드시 0과 1 사이의 숫자여야 합니다. 여기서 0은 절대, 1은 항상을 의미합니다.
통계에서는 이 "얼마나 자주"를 "p-값"이라고 합니다.
이 시점에서 추론 방식은 매우 간단 합니다. p-값이 매우 낮으면 원래 가설이 틀릴 가능성이 있음을 의미합니다.
"예기치 않음"의 개념은 테스트 중인 특정 가설에 밀접하게 의존합니다. 예를 들어, 주사위가 공정하다고 생각한다면 결과 [2, 2, 2, 2, 2, 4]가 꽤 이상합니다. 그러나 주사위가 로드되어 시간의 75%에서 숫자 "2"를 얻는다고 생각하면 그다지 놀라운 일이 아닙니다.
통계 테스트의 구성 요소
이전 단락을 읽으면 두 가지 구성 요소가 필요하다고 추측했을 수 있습니다.
- 귀무 가설에 따른 가능한 결과의 분포.
- 결과의 "예상치 못한" 정도를 측정합니다.
첫 번째 성분과 관련하여 결과의 전체 분포를 얻는 것이 항상 간단한 것은 아닙니다. 종종 많은 수의 결과를 무작위로 시뮬레이션하는 것이 더 편리하고 더 쉽습니다 . 이것은 실제 분포에 대한 좋은 근사치입니다.
두 번째 요소에 대해 가능한 각 결과를 단일 숫자로 매핑하는 함수 를 정의해야 합니다 . 이 숫자는 귀무 가설이 참인 경우 결과가 얼마나 예상치 못한지 표현해야 합니다. 예상치 못한 결과가 많을수록 이 점수가 높아집니다.
이 두 가지 재료가 있으면 기본적으로 작업이 완료된 것입니다. 실제로 분포에서 각 결과의 의외성 점수와 관찰된 결과의 의외성 점수를 계산하는 것으로 충분합니다.
p-값은 관찰된 점수보다 높은 무작위 점수의 백분율입니다.
그게 다야 이것이 모든 단일 통계 테스트가 내부적으로 작동하는 방식입니다.
다음은 방금 설명한 프로세스를 그래픽으로 나타낸 것입니다.

독특한 통계 테스트
하지만 파이썬에서는 어떻게 할까요? 알고리즘은 다음과 같습니다.
- 함수를 정의합니다 draw_random_outcome. 이 함수는 귀무 가설이 참인 경우 무작위 시행의 결과를 반환해야 합니다. 단일 숫자, 배열, 배열 목록, 이미지, 거의 모든 것이 될 수 있습니다. 특정 경우에 따라 다릅니다.
- 함수를 정의합니다 unexp_score("예상치 못한 점수"를 나타냄). 함수는 실험 결과를 입력으로 가져와 단일 숫자를 반환해야 합니다. 이 숫자는 귀무 가설에서 생성되었다고 가정할 때 결과가 얼마나 예상치 못한지에 대한 점수여야 합니다. 점수는 양수, 음수, 정수 또는 부동 소수점일 수 있으며 중요하지 않습니다. 반드시 가져야 하는 유일한 속성은 다음과 같습니다. 결과가 희박할수록 이 점수는 높아야 합니다 .
- 함수(포인트 1에서 정의됨)를 여러 번(예: 10,000번) 실행하고 draw_random_outcome각 임의 결과에 대해 해당 함수( unexp_score포인트 2에서 정의됨)를 계산합니다. 라는 배열에 모든 점수를 저장합니다 random_unexp_scores.
- 관찰된 결과를 계산 unexp_score하고 이라고 합니다 observed_unexp_score.
- 관찰된 결과보다 예상치 못한 무작위 결과가 얼마나 많은지 계산합니다. 즉, random_unexp_scores보다 높은 요소의 수를 세 observed_unexp_score십시오. 이것은 p-값입니다.
처음 두 단계는 특정 경우에 따라 약간의 창의성이 필요한 유일한 단계이며 3, 4 및 5단계는 순전히 기계적입니다.
이제 좀 더 구체적으로 설명하기 위해 예제를 살펴보겠습니다.
예 1. 주사위 굴리기
우리는 주사위를 10번 발사했고 다음과 같은 결과를 얻었습니다.
observed_outcome = np.array([1,1,1,1,1,2,2,2,3,3])
귀무 가설은 주사위가 공정하다는 것입니다. 이 가설에 따르면 임의의 결과를 쉽게 추출할 수 있습니다. Numpy를 사용하는 것으로 충분합니다 random.choice. 이것이 알고리즘의 첫 번째 단계입니다.
# step 1
def draw_random_outcome():
return np.random.choice([1,2,3,4,5,6], size=10)
unexp_score두 번째 단계는 각각의 가능한 결과에 예상치 못한 점수를 할당해야 하는 함수를 정의하는 것 입니다.
주사위가 공정하다면 각 면이 평균 1/6 시간에 나타날 것으로 예상합니다. 따라서 각 면의 관찰 주파수와 1/6 사이의 거리를 확인해야 합니다. 그런 다음 단일 점수를 얻으려면 평균을 취해야 합니다. 이런 식으로 1/6에서 평균 거리가 높을수록 더 예상치 못한 결과가 나옵니다.
# step 2
def unexp_score(outcome):
outcome_distribution = np.array([np.mean(outcome == face) for face in [1,2,3,4,5,6]])
return np.mean(np.abs(outcome_distribution - 1/6))
이 시점에서 어려운 부분은 완료되었습니다. 이전에 말했듯이 알고리즘의 3, 4, 5단계는 완전히 기계적입니다.
# step 3
n_iter = 10000
random_unexp_scores = np.empty(n_iter)
for i in range(n_iter):
random_unexp_scores[i] = unexp_score(draw_random_outcome())
# step 4
observed_unexp_score = unexp_score(observed_outcome)
# step 5
pvalue = np.sum(random_unexp_scores >= observed_unexp_score) / n_iter
결과 p-값은 1.66%이며, 이는 귀무 가설에서 결과의 1.66%만이 [1,1,1,1,1,2,2,2,3,3]만큼 예상치 못한 결과임을 의미합니다.
이상하게도 예상치 못한 점수의 분포와 관찰된 점수가 정확히 어디에 속하는지 보여주는 히스토그램입니다.
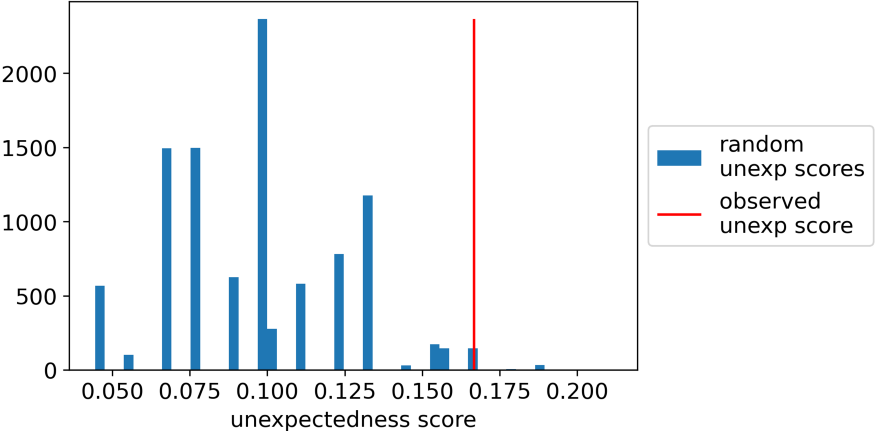
예 2. 스크래블 미스터리
당신의 친구는 가방에서 일부 스크래블 타일이 떨어졌고 우연히 그 글자가 "FEAR"라는 실제 단어를 형성했다고 주장합니다. 당신은 당신의 친구가 당신을 놀리고 있다고 의심합니다. 친구가 거짓말을 하는지 통계적으로 확인하는 방법은 무엇입니까?
우선 관찰된 결과는 일련의 문자이므로 문자열입니다.
observed_outcome = 'FEAR'
가방에 알파벳 26자가 들어 있다고 가정합니다. 귀무 가설은 임의의 숫자(1에서 26 사이)의 문자가 무작위 순서로 가방에서 떨어졌다는 것입니다. random따라서 문자 수와 문자 선택 모두에 Numpy를 사용해야 합니다.
# step 1
def draw_random_outcome():
size=np.random.randint(low=1, high=27)
return ''.join(np.random.choice(list(string.ascii_uppercase), size=size, replace=False))
이제 이 시나리오에서 예기치 않은 상황을 평가하는 방법은 무엇입니까?
일반적으로 가방에서 떨어지는 글자가 많을수록 실제 단어를 얻을 가능성은 낮아질 것으로 예상하는 것이 합리적입니다.
따라서 이 규칙을 사용할 수 있습니다. 문자열이 기존 단어인 경우 점수는 단어의 길이가 됩니다. 문자열이 실제 단어가 아니면 점수는 단어의 길이를 뺀 값입니다.
이것이 알고리즘의 2단계입니다(참고: pip install english-words아래 코드가 작동하도록 해야 합니다).
# step 2
from english_words import english_words_set
english_words_set = [w.upper() for w in english_words_set]
def unexp_score(outcome):
is_in_dictionary = outcome in english_words_set
return (1 if is_in_dictionary else -1) * len(outcome)
3, 4, 5단계는 항상 동일하므로 이전 예제에서 복사하여 붙여넣습니다.
# step 3
n_iter = 10000
random_unexp_scores = np.empty(n_iter)
for i in range(n_iter):
random_unexp_scores[i] = unexp_score(draw_random_outcome())
# step 4
observed_unexp_score = unexp_score(observed_outcome)
# step 5
pvalue = np.sum(random_unexp_scores >= observed_unexp_score) / n_iterThis is the result:
결과는 다음과 같습니다.
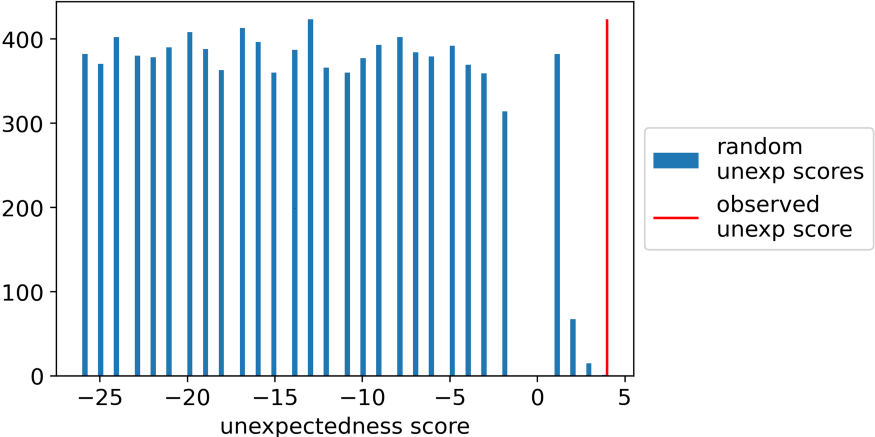
이 경우 관찰된 점수보다 높은 임의 점수가 없었으므로 p-값은 0.0입니다. 그래서, 이 통계적 테스트에 따르면, 당신의 친구는 거짓말을 하고 있었습니다!
그렇다면 왜 그 모든 통계적 테스트가 필요할까요?
여기까지 왔다면 다음과 같은 질문을 할 수 있습니다. 그렇게 쉬운데 왜 그렇게 많은 테스트가 존재합니까? 대답은 대부분 "역사적"입니다.
계산이 지금보다 훨씬 더 비쌌던 시절이 있었기 때문에 "통계 테스트"는 기본적으로 p-값을 효율적으로 계산하는 지름길이었습니다. 그리고 우리가 본 알고리즘의 1단계와 2단계를 선택할 가능성이 너무 많기 때문에 테스트가 급증했습니다.
이 주제를 심화하고 싶다면 이 기사에 영감을 준 앨런 다우니 의 고전 "테스트는 하나만 있습니다" 를 읽을 수 있습니다.
'Daily Review' 카테고리의 다른 글
| LSTM AE를 활용한 이상 탐지 프로젝트 (0) | 2022.09.01 |
|---|---|
| Autoencoder를 활용한 이미지 이상 탐지 (0) | 2022.08.31 |
| 스파게티 차트(Spaghetti Charts) 대신 제안된 대안: 격자 차트(Trellis Chart) (0) | 2022.08.31 |
| An End-to-End Unsupervised Anomaly Detection (0) | 2022.08.30 |
| SQL을 사용한 레스토랑 판매의 탐색적 데이터 분석(EDA) (3) | 2022.08.30 |




댓글