
아래 2가지 상황을 경험해본 적 있을 것이다.
- 모델이 원하는 대로 작동하지 않습니다.
- 일부 포인트가 나머지 포인트와 크게 다르다는 사실에 주목하지 않을 수 없습니다.
이런 상황이라면, 아마도 데이터에 이상치가 있다는 거다.
이상치란 무엇입니까?
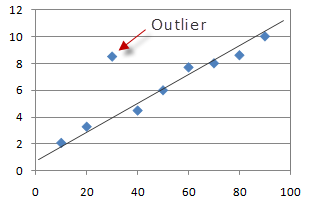
통계에서 이상치는 다른 관측치와 크게 다른 데이터입니다. 위의 그림에서 우리는 대부분의 점이 선형 초평면 안에 있고 그 주위에 있지만 단일 점이 나머지 부분에서 발산하는 것을 볼 수 있음을 분명히 알 수 있습니다. 이 점은 이상치 입니다.
예를 들어 아래 목록을 살펴보십시오.
[ 1,35,20,32,40,46,45 , 4500 ]여기에서 1과 4500이 데이터 세트의 이상값임을 분명히 쉽게 알 수 있습니다.
내 데이터에 이상치가 있는 이유는 무엇입니까?
일반적으로 이상치는 다음 시나리오 중 하나에서 발생할 수 있습니다.
- 때로는 측정 오류로 인해 우연히 발생할 수 있습니다.
- 데이터가 이상값 없이 100% 깨끗한 경우는 거의 없기 때문에 때때로 데이터에서 발생할 수 있습니다.
이상치가 왜 문제인가?
1. 선형 모델
일부 데이터가 있고 선형 회귀를 사용하여 이 데이터에서 주택 가격을 예측하려고 한다고 가정해 보겠습니다. 가능한 가설은 다음과 같습니다.
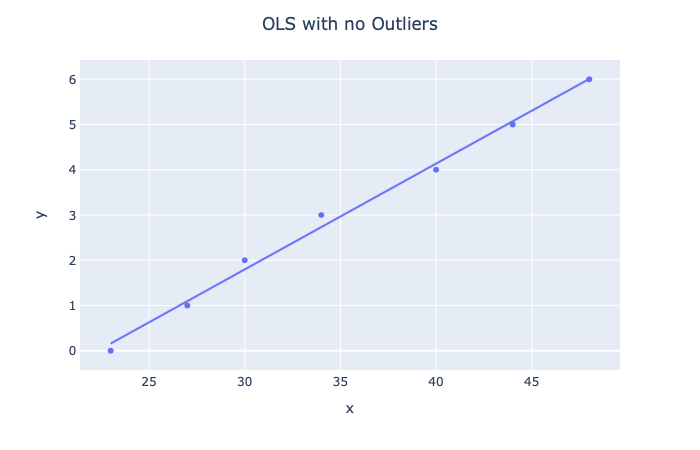
이 경우 실제로 데이터를 너무 잘 피팅( 과적합 )하고 있습니다. 그러나 모든 포인트가 대략적으로 같은 범위에 위치하는 방법에 유의하십시오.
이제 이상치를 추가할 때 어떤 일이 발생하는지 봅시다.
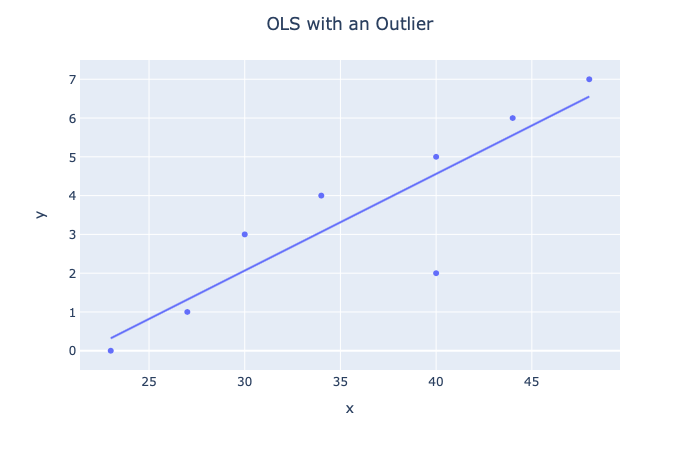
분명히 우리는 우리의 가설이 어떻게 이동했는지 알 수 있습니다. 따라서 추론은 이상치가 없을 때보다 훨씬 더 나빠질 것입니다. 선형 모델에는 다음이 포함됩니다.
- 퍼셉트론
- 선형 + 로지스틱 회귀
- 신경망
- KNN
2. 데이터 입력

일반적인 시나리오는 데이터가 누락되는 것이며 두 가지 접근 방식 중 하나를 사용할 수 있습니다.
- 행이 누락된 인스턴스 제거
- 통계적 방법을 사용하여 데이터 대치
두 번째 옵션을 사용한다면 이상치가 통계적 방법의 값을 크게 변경할 수 있으므로 문제가 있는 전가를 가질 수 있습니다. 예를 들어 이상값이 없는 가상 데이터로 돌아가면 다음과 같습니다.
# 이상값이 없는 데이터
np.array([35,20,32,40,46,45]).mean() = 36.333333333333336 # 2개의 이상치가 있는 데이터
np.array([1,35,20,32,40,46,45,4500]).mean() = 589.875
분명히 이 예시는 매우 극단적이지만 아이디어는 동일하게 유지됩니다. 데이터의 이상치는 일반적으로 문제입니다. 이상치는 통계 분석 및 모델링에서 심각한 문제를 일으킬 수 있기 때문입니다. 그러나 이 기사에서는 이를 감지하고 대처하는 방법에 대해 몇 가지 방법을 살펴볼 것입니다.
솔루션 1: DBSCAN

잡음이 있는 애플리케이션의 밀도 기반 공간 클러스터링(또는 더 간단하게는 DBSCAN)은 실제로 KMeans와 마찬가지로 감독되지 않은 클러스터링 알고리즘입니다. 그러나 그 용도 중 하나는 데이터에서 이상값을 감지할 수도 있다는 것입니다.
DBSCAN은 KMeans 및 Gaussian Mixtures로 수행할 수 없는 비선형 분리 가능한 클러스터를 찾을 수 있기 때문에 인기가 있습니다. 클러스터와 밀도가 충분할 때 잘 작동하며 밀도가 낮은 영역으로 분리되어 있습니다.
DBSCAN 작동 방식에 대한 개요
알고리즘은 클러스터를 고밀도의 연속 영역으로 정의합니다. 알고리즘은 매우 간단합니다.
- 각 인스턴스에 대해 몇 개의 인스턴스가 그로부터 작은 거리 ε(엡실론) 내에 있는지 계산합니다. 이 영역을 인스턴스의 ε- 이웃이라고 합니다.
- 인스턴스의 ε-neighbourhood에 min_samples 개 이상의 인스턴스가 있는 경우 코어 인스턴스 로 간주됩니다 . 이는 인스턴스가 고밀도 영역(내부에 인스턴스가 많은 영역)에 위치한다는 것을 의미합니다.
- 코어 인스턴스의 ε-neighbourhood 내부의 모든 인스턴스는 동일한 클러스터에 할당됩니다. 여기에는 다른 코어 인스턴스가 포함될 수 있으므로 인접한 코어 인스턴스의 긴 단일 시퀀스가 단일 클러스터를 형성합니다.
- 코어 인스턴스가 아니거나 코어 인스턴스의 ε-이웃에 없는 모든 인스턴스는 이상값입니다.
DBSCAN 알고리즘 구현
DBSCAN 알고리즘은 Scikit-Learn의 직관적인 API 덕분에 매우 사용하기 쉽습니다. 작동 중인 알고리즘의 예를 살펴보겠습니다.
from sklearn.cluster import DBSCAN
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=1000, noise=0.05)
dbscan = DBSCAN(eps=0.2, min_samples=5)
dbscan.fit(X)
여기서 우리는 0.05의 ε-이웃 길이로 DBSCAN을 인스턴스화하고 5는 인스턴스가 코어 인스턴스로 간주되는 데 필요한 최소 샘플 수입니다.
비지도 알고리즘 이므로 레이블을 전달하지 않는다는 것을 기억하십시오 . 다음 명령을 사용하여 알고리즘이 생성한 레이블을 볼 수 있습니다.
dbscan.labels_
OUT:
array([ 0, 2, -1, -1, 1, 0, 0, 0, ..., 3, 2, 3, 3, 4, 2, 6, 3])
일부 레이블의 값이 -1인 방법에 유의하십시오. 이는 이상값입니다.
DBSCAN에는 예측 방법이 없고 fit_predict 방법만 있으므로 새 인스턴스를 클러스터링할 수 없습니다. 대신 다른 분류기를 사용하여 학습하고 예측할 수 있습니다. 이 예에서는 KNN을 사용하겠습니다.
from sklearn.neighbors import KNeighborsClassifier
knn = KNeighborsClassifier(n_neighbors=50)
knn.fit(dbscan.components_, dbscan.labels_[dbscan.core_sample_indices_])
X_new = np.array([[-0.5, 0], [0, 0.5], [1, -0.1], [2, 1]])
knn.predict(X_new)
OUT:
array([1, 0, 1, 0])
여기에서 핵심 샘플과 해당 이웃에 KNN 분류기를 맞춥니다.
그러나 우리는 한 가지 문제에 봉착합니다. 이상치 없이 KNN 데이터를 제공했습니다. 이는 새 인스턴스가 실제로 이상값이더라도 KNN이 새 인스턴스에 대한 클러스터를 선택하도록 강제하기 때문에 문제가 됩니다.
이를 방지하기 위해 우리는 KNN 분류기의 kneighbors 방법을 활용합니다. 이 방법은 인스턴스 세트가 주어지면 훈련 세트의 k개의 최근접 이웃의 거리와 인덱스를 반환합니다. 그런 다음 최대 거리를 설정할 수 있으며 인스턴스가 해당 거리를 초과하면 이상값으로 규정합니다.
y_dist, y_pred_idx = knn.kneighbors(X_new, n_neighbors=1)
y_pred = dbscan.labels_[dbscan.core_sample_indices_][y_pred_idx]
y_pred[y_dist > 0.2] = -1
y_pred.ravel()
OUT:
array([-1, 0, 1, -1])
여기에서 이상 탐지를 위한 DBSCAN에 대해 논의하고 구현했습니다. DBSCAN은 빠르고, 하이퍼파라미터가 2개뿐이며, 이상치에 대해 강력하기 때문에 훌륭합니다.
솔루션 2: IsolationForest

IsolationForest는 앙상블 학습 이상 감지 알고리즘으로, 고차원 데이터 세트에서 이상값을 감지하는 데 특히 유용합니다.알고리즘은 기본적으로 다음을 수행합니다.
- 결정 트리가 무작위로 성장하는 랜덤 포레스트를 생성합니다. 각 노드에서 기능이 무작위로 선택되고 데이터 세트를 두 개로 분할하기 위해 임의의 임계값을 선택합니다.
- 모든 인스턴스가 서로 격리될 때까지 데이터 세트를 계속 잘라냅니다.
- 이상 현상은 일반적으로 다른 인스턴스와 멀리 떨어져 있으므로 평균적으로(모든 의사 결정 트리에서) 일반 인스턴스보다 더 적은 단계로 격리됩니다.
IsolationForest 알고리즘 구현
다시 말하지만, Scikit-Learn의 직관적인 API 덕분에 IsolationForest 클래스를 쉽게 구현할 수 있습니다. 작동 중인 알고리즘의 예를 살펴보겠습니다.
from sklearn.ensemble import IsolationForest
from sklearn.metrics import mean_absolute_error
import pandas as pd
우리는 또한 우리의 오류를 측정하기 위해 mean_absolute_error를 가져올 것입니다. 데이터의 경우 Jason Brownlee의 GitHub 에서 얻을 수 있는 데이터 세트를 사용합니다 .
url='https://raw.githubusercontent.com/jbrownlee/Datasets/master/housing.csv'
df = pd.read_csv(url, header=None)
data = df.values
# split into input and output elements
X, y = data[:, :-1], data[:, -1]
Isolation Forest를 적용하기 전에 데이터에 기본 선형 회귀 모델을 적용하고 MAE를 구해 보겠습니다.
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(X,y)
mean_absolute_error(lr.predict(X),y)
OUT:
3.2708628109003177
비교적 좋은 점수. 이제 Isolation Forest가 변칙성을 제거하여 점수를 향상시킬 수 있는지 봅시다!
먼저 IsolationForest를 인스턴스화합니다.
iso = IsolationForest(contamination='auto',random_state=42)
알고리즘에서 가장 중요한 하이퍼파라미터는 아마도 데이터세트의 이상치 수를 추정하는 데 사용되는 오염 파라미터일 것입니다. 0.0에서 0.5 사이의 값이며 기본적으로 0.1로 설정되어 있습니다.
그러나 이것은 본질적으로 무작위화된 랜덤 포레스트이므로 랜덤 포레스트의 모든 하이퍼파라미터도 알고리즘에서 사용할 수 있습니다.
다음으로 데이터를 알고리즘에 학습시킵니다.
y_pred = iso.fit_predict(X,y)
mask = y_pred != -1
DBSCAN에서와 같이 예측 값 = -1도 필터링하는 방법에 유의하십시오. 이는 이상값으로 간주됩니다.
이제 이상치 필터링된 데이터로 X와 Y를 재할당합니다.
X,y = X[mask,:],y[mask]
이제 선형 회귀 모델을 데이터에 맞추고 MAE를 측정해 보겠습니다.
lr.fit(X,y)
mean_absolute_error(lr.predict(X),y)
OUT:
2.643367450077622
와우~ 비용절감이 좋네요. 이것은 Isolation Forest의 위력을 분명히 보여줍니다.
솔루션 3: 상자 그림 + 터키 방법
Boxplots는 이상값을 식별하는 매우 일반적인 방법이지만 실제로 후자는 이상값을 식별하는 가장 과소평가된 방법일 수 있습니다. 그러나 터키 방법을 시작하기 전에 Boxplots에 대해 이야기합시다.
Boxplot

Boxplots는 기본적으로 분위수를 통해 숫자 데이터를 표시하는 그래픽 방식을 제공합니다. 이상값을 시각화하는 매우 간단하면서도 효과적인 방법입니다.
위쪽 및 아래쪽 수염은 분포의 경계를 나타내며 위 또는 아래는 이상값으로 간주됩니다. 위의 그림에서 ~80 이상과 ~62 미만은 모두 이상값으로 간주됩니다.
Boxplot 작동 방식
기본적으로 상자 그림은 데이터 세트를 5개 부분으로 분할하여 작동합니다.
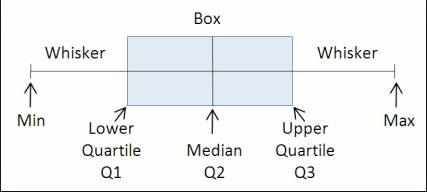
- Min : 이상치를 제외한 분포에서 가장 낮은 데이터 포인트.
- Max : 이상값을 제외한 분포에서 가장 높은 데이터 포인트.
- 중앙값( Q 2 / 50번째 백분위수) : 데이터 세트의 중간 값입니다.
- 1사분위수( Q 1 / 25번째 백분위수) : 데이터 세트의 하위 절반의 중앙값입니다.
- 3사분위수( Q3 / 75번째 백분위수) : 데이터 세트의 상위 절반의 중앙값입니다.
사분위수 범위(IQR)는 이상치를 정의하기 때문에 중요합니다. 기본적으로 다음과 같습니다.
IQR = Q3 - Q1
Q3: third quartile
Q1: first quartile
상자 그림에서 1.5 * IQR의 거리가 측정되고 데이터 세트의 더 높은 관찰 지점을 포함합니다. 유사하게, 1.5 * IQR의 거리는 데이터 세트의 더 낮은 관찰 지점에서 측정됩니다. 이 거리를 벗어나는 것은 모두 이상값입니다. 더 구체적으로:
- 관찰된 점이 (Q1 − 1.5 * IQR) 미만이거나 boxplot 더 낮은 수염인 경우 이상값으로 간주됩니다.
- 마찬가지로 관찰된 점이 (Q3 + 1.5 * IQR) 또는 boxplot 상단 수염 위에 있는 경우에도 이상값으로 간주됩니다.
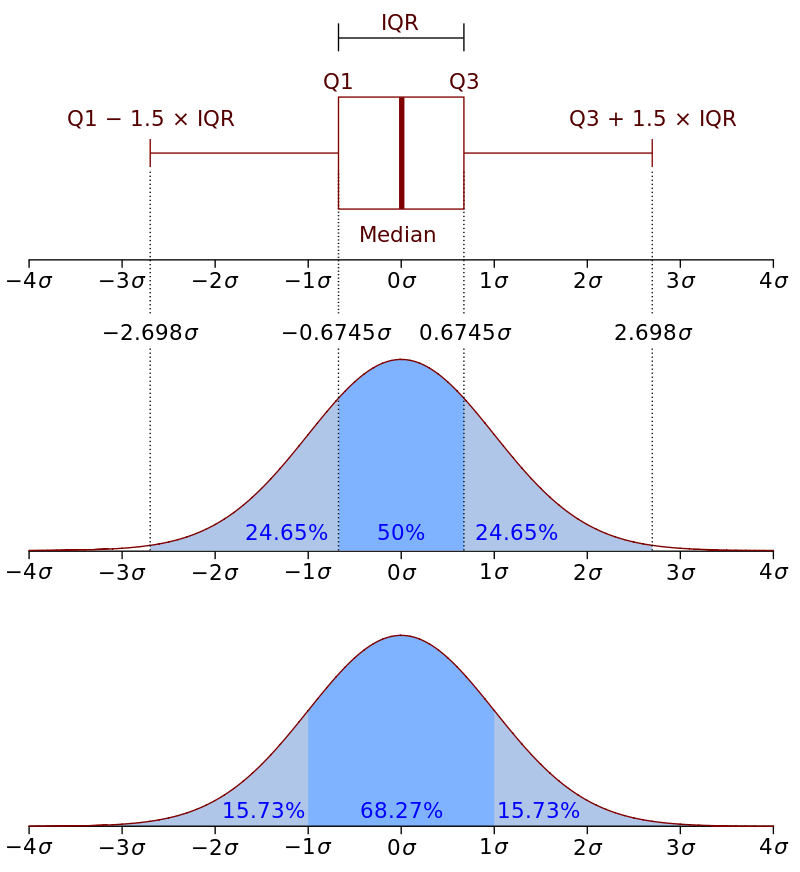
상자 그림 구현
Python에서 Boxplots를 사용하여 이상값을 감지하는 방법을 살펴보겠습니다!
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
X = np.array([45,56,78,34,1,2,67,68,87,203,-200,-150])
y = np.array([1,1,0,0,1,0,1,1,0,0,1,1])
데이터의 상자 그림을 그려 보겠습니다.
sns.boxplot(X)
plt.show()
따라서 상자 그림에 따르면 데이터에 중앙값 50과 3개의 이상값이 있음을 알 수 있습니다. 이러한 점을 제거합시다.
X = X[(X < 150) & (X > -50)]
sns.boxplot(X)
plt.show()
여기서는 기본적으로 임계값을 설정하여 -50보다 작거나 150보다 큰 모든 포인트가 제외됩니다. 그리고 결과; 균등 분배!
터키 방법 이상값 탐지
터키 방법 이상값 감지는 실제로 상자 그림의 비시각적 방법입니다. 방법은 시각화가 없다는 점을 제외하고는 동일합니다.
내가 때때로 boxplot과 반대로 이 방법을 선호하는 이유는 때때로 시각화를 살펴보고 임계값을 설정해야 하는 대략적인 추정을 하는 것이 실제로 효과적이지 않기 때문입니다.
대신에 이상치로 정의한 인스턴스를 실제로 반환할 수 있는 알고리즘을 코딩할 수 있습니다.
구현을 위한 코드는 다음과 같습니다.
import numpy as np
from collections import Counter
def detect_outliers(df, n, features):
# list to store outlier indices
outlier_indices = []
# iterate over features(columns)
for col in features:
# Get the 1st quartile (25%)
Q1 = np.percentile(df[col], 25)
# Get the 3rd quartile (75%)
Q3 = np.percentile(df[col], 75)
# Get the Interquartile range (IQR)
IQR = Q3 - Q1
# Define our outlier step
outlier_step = 1.5 * IQR
# Determine a list of indices of outliers
outlier_list_col = df[(df[col] < Q1 - outlier_step) | (df[col] > Q3 + outlier_step)].index
# append outlier indices for column to the list of outlier indices
outlier_indices.extend(outlier_list_col)
# select observations containing more than 2 outliers
outlier_indices = Counter(outlier_indices)
multiple_outliers = list(k for k, v in outlier_indices.items() if v > n)
return multiple_outliers
# detect outliers from list of features
list_of_features = ['x1', 'x2']
# params dataset, number of outliers for rejection, list of features Outliers_to_drop = detect_outliers(dataset, 2, list_of_features)
기본적으로 이 코드는 다음을 수행합니다.
- 모든 기능에 대해 다음을 얻습니다.
- 1사분위수
- 3사분위수
- IQR
2. 다음 으로 boxplots에서와 같이 1.5 * IQR인 이상치 단계를 정의합니다.
3. 다음과 같은 방법으로 이상값을 감지합니다.
- 관찰된 점이 < Q1인지 확인 - 이상치 단계
- 관찰된 점이 Q3 + 이상치 단계인지 확인
4. 그런 다음 k 이상값(이 경우 k = 2)이 있는 관측값을 선택합니다.
결론
요약하자면, 많은 이상치 탐지 알고리즘이 존재하지만 가장 일반적인 3가지 알고리즘인 DBSCAN, IsolationForest 및 Boxplots를 살펴보았습니다. 다음을 수행하도록 권장합니다.
- Titanic Dataset에서 다음 방법을 시도하십시오. 어느 것이 이상치를 가장 잘 감지합니까?
- 다른 이상값 탐지 방법을 찾아 처음에 시도한 방법보다 성능이 더 좋은지 나쁜지 확인합니다.
나는 나의 추종자들에게 정말로 감사하고, 나는 끊임없이 글을 쓰고 모든 사람들에게 생각할 거리를 제공하기를 희망합니다. 그러나 지금은 작별인사를 해야 합니다 ;}
'Daily Review' 카테고리의 다른 글
| model.fit() 데이터 사이언티스트를 위한 자리는 없습니다. (0) | 2022.09.02 |
|---|---|
| "Isolation Forest": 모든 데이터 분석가가 알아야 할 이상 탐지 알고리즘 (0) | 2022.09.02 |
| Data-Driven Organization을 향한 디자인 씽킹 (0) | 2022.09.01 |
| LSTM AE를 활용한 이상 탐지 프로젝트 (0) | 2022.09.01 |
| Autoencoder를 활용한 이미지 이상 탐지 (0) | 2022.08.31 |




댓글