
"Isolation Forest"는 2009년에 탄생한 뛰어난 이상 탐지 알고리즘입니다( 여기 에 원본 논문이 있습니다). 이후 매우 유명해졌습니다. Scikit-learn에서도 구현됩니다( 문서 참조 ).
이 기사에서 우리는 이 알고리즘 뒤에 숨겨진 직관의 아름다움에 감사하고 몇 가지 예를 통해 내부에서 정확히 어떻게 작동하는지 이해할 것입니다.
"이상 탐지가 왜 그렇게 어려운가요?"
이상(또는 이상치) 탐지는 대부분의 관찰과 비교하여 "매우 이상한" 데이터 포인트를 식별하는 작업입니다.
이는 결함 감지에서 금융 사기 발견, 건강 문제 발견에서 불만족 고객 식별에 이르기까지 다양한 응용 분야에서 유용합니다. 또한 이상값을 제거하면 모델 정확도가 증가한다는 것이 입증 되었기 때문에 기계 학습 파이프라인에도 유용할 수 있습니다 .
이상 탐지를 어렵게 만드는 것은 감독되지 않은 문제라는 점입니다. 즉, 일반적으로 어떤 인스턴스가 실제로 "변칙"인지 알려주는 레이블이 없습니다. 또는 레이블이 있더라도 이상 감지를 감독된 문제로 프레임화하는 것은 매우 어려울 것입니다. 사실로:
- 예외는 드뭅니다.
- 이상 현상은 새로운 것입니다.
- 이상은 서로 다릅니다.
이러한 모든 이유로 감독 기술은 일반적으로 이상 탐지에 적합하지 않습니다.
Isolation Forest의 특별한 점
이상 탐지에 대한 전통적인 접근 방식은 대략 다음과 같습니다.
- "일반 인스턴스"가 어떻게 생겼는지 설명하십시오(일반적으로 클러스터 분석이 포함됨).
- 해당 프로필에 맞지 않는 모든 인스턴스에 이상값으로 레이블을 지정합니다.
Isolation Forest가 도입한 혁신은 정상적인 관찰이 아닌 이상치에서 직접 시작한다는 것입니다.
핵심 아이디어는 이상을 독특하게 만드는 특성을 기반으로 이상을 "분리"하는 것이 매우 쉬워야 한다는 것입니다.
기술적으로 이것은 다음과 같은 사실로 해석됩니다.모든 관찰에 대해 결정 트리를 맞추면 "정상" 인스턴스보다 트리의 루트에 더 가까운 이상값을 찾아야 합니다.
무슨 뜻인가요? 예를 들어 이것을 명확히 합시다.
현재 살아있는 7,932,843,214명의 모든 인간에 대한 데이터를 포함하는 데이터 세트가 있다고 가정합니다. 나이, 순자산, 거주지, 직위 등 원하는 만큼 많은 변수가 있습니다.
그러한 데이터 세트의 이상치는 무엇입니까? 이상치는 반드시 잘못된 데이터가 아님을 명심하십시오. 이는 나머지 모집단과 매우 다른 데이터 포인트일 뿐입니다. 이 예에서 Jeff Bezos는 확실히 이상치입니다.
이제 각 터미널 리프에 단 한 사람만 포함되도록 결정 트리를 맞출 수 있다고 상상해 보십시오. 즉, 이 나무는 가지치기가 완전히 되지 않습니다. Isolation Forest 뒤에 있는 가정이 맞다면 Jeff Bezos는 나 자신보다 나무 뿌리에 더 가깝습니다.
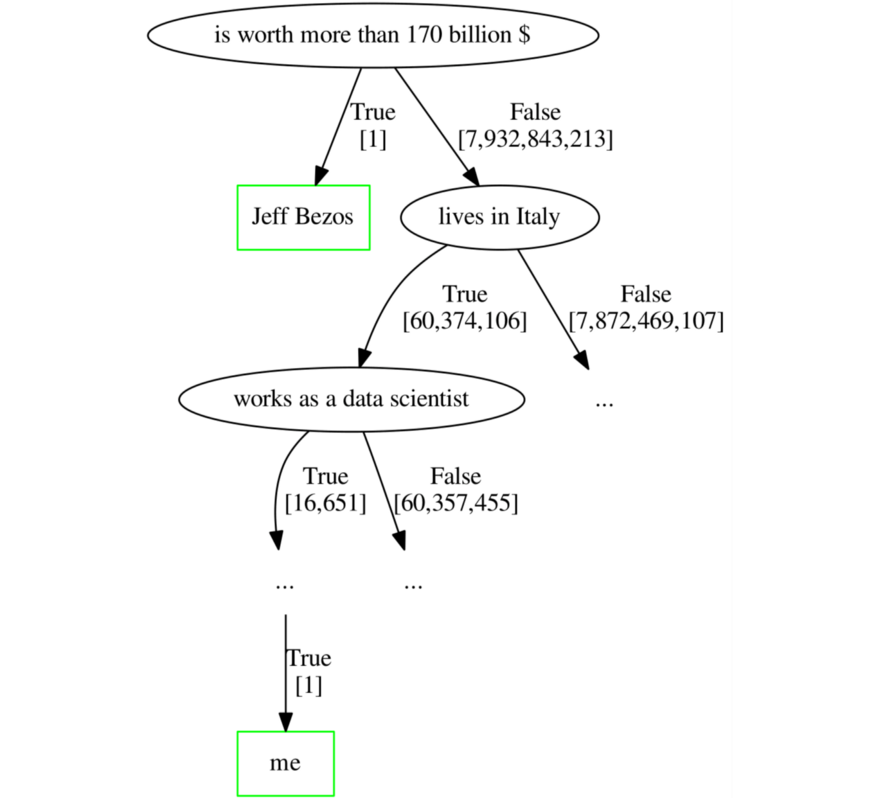
이상치이기 때문에 Jeff Bezos는 분리하기가 더 쉽습니다. "그가 1,700억 달러 이상의 가치가 있습니까?"라고 묻는 것으로 충분합니다. 거의 80억 명의 인간 중에서 그를 되찾기 위해. 반면에 나는 Jeff Bezos보다 훨씬 더 평범하기 때문에 당신이 나를 찾을 때까지 검색 공간을 좁히려면 적어도 10개의 참/거짓 질문이 필요할 것입니다.
예시
이제 Isolation Forest 뒤에 있는 주요 직관을 보았으므로 몇 가지 간단한 데이터를 사용하여 알고리즘의 정확한 역학을 이해하려고 합니다.
import pandas as pd
df = pd.DataFrame({
'x': [1.0, 1.1, 1.2, 1.3, 1.4, 1.5, 2.0],
'y': [2.1, 2.4, 3.0, 2.6, 2.2, 2.8, 3.7]
}, index = ['A', 'B', 'C', 'D', 'E', 'F', 'G'])
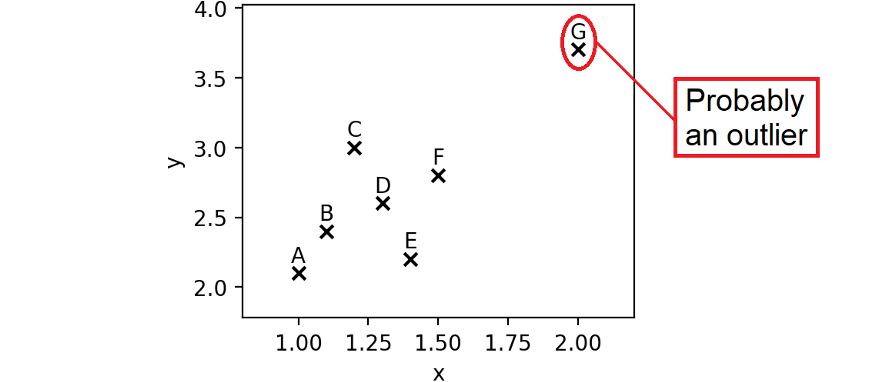
A에서 F까지의 항목은 "정상적인" 데이터 포인트인 매우 컴팩트한 포인트 클라우드를 나타냅니다. 이러한 경우와 비교할 때 G는 아마도 이상값일 것입니다. x 및 y 모두에 비정상적인 값이 있습니다 .
Isolation Forest는 트리를 기반으로 하므로 다음 데이터에 트리를 맞추겠습니다.
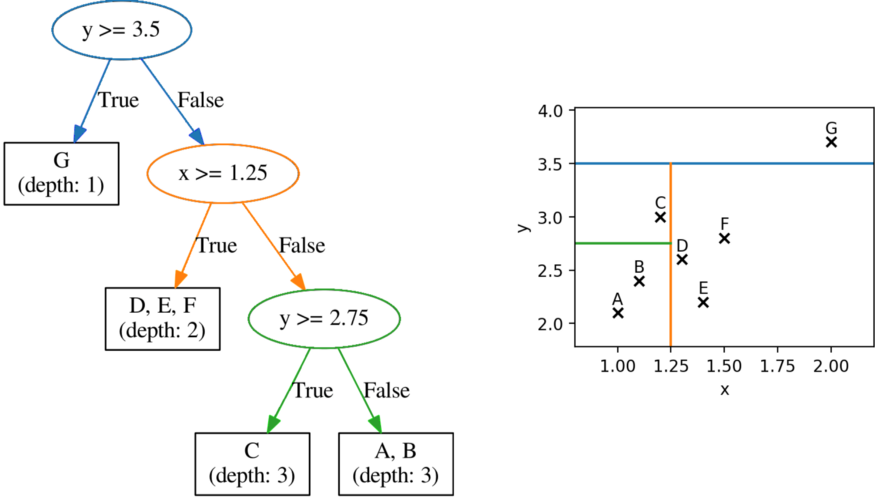
이 나무는 무작위 방식으로 성장했습니다.
여기서 가장 기본적인 개념은 각 요소가 발견되는 잎의 깊이입니다 . 예를 들어, 이 트리에서 G(우리의 이상치)라는 관측치는 깊이 1(예: 루트 노드에서 1 수준)에 있는 반면 C는 깊이 3에 있습니다.
Isolation Forest 뒤에 있는 아이디어는 평균적으로 이상값이 일반 인스턴스보다 루트 노드에 더 가깝다는 것입니다(즉, 더 낮은 깊이에서).
머신 러닝에서 흔히 그렇듯이 핵심은 반복입니다. 실제로 많은 결정 트리를 무작위로 맞춘 다음 다른 트리에 대한 각 관찰의 평균을 취하면 "이상치"의 경험적 측정을 나타내는 "평균 깊이"를 찾습니다.
Scikit-learn의 Isolation Forest
Scikit-learn의 구현을 통한 사용 예를 살펴보겠습니다.
from sklearn.ensemble import IsolationForest
iforest = IsolationForest(n_estimators = 100).fit(df)
숲( iforest.estimators_[:9])에서 처음 9개의 나무를 가져와 그려보면 다음과 같습니다.
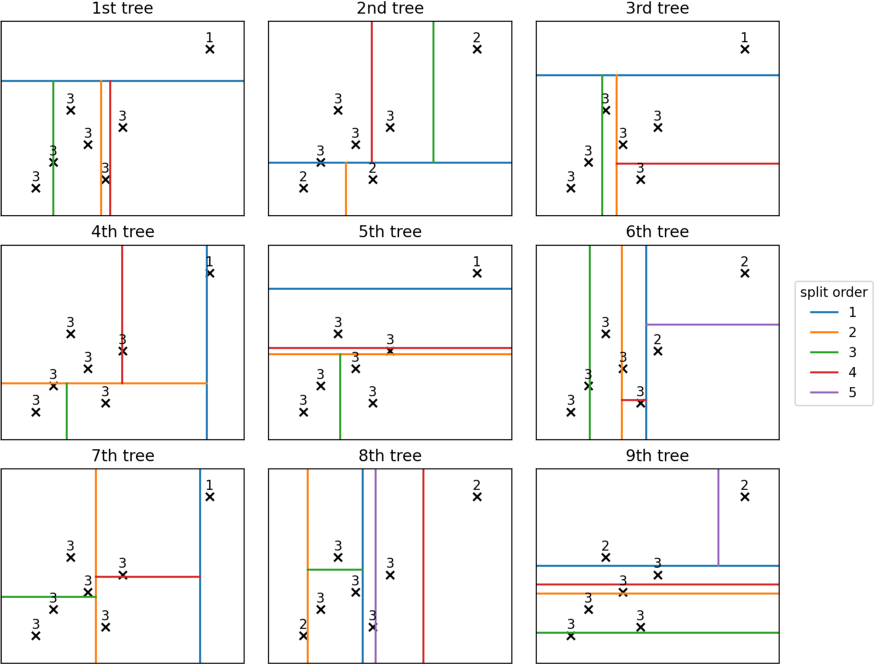
이 처음 9개의 트리를 살펴보면 이미 패턴을 볼 수 있습니다. G는 다른 지점보다 훨씬 낮은 깊이(평균 1.44)에 있는 경향이 있습니다. 실제로 두 번째 점은 평균 깊이가 2.78인 A입니다.
개념적으로 이것이 바로 알고리즘이 작동하는 방식입니다. 평균 깊이가 낮을수록 이상값이 될 가능성이 높아집니다.
그러나 실제로는 평균 깊이를 사용할 수 없습니다. 트리의 깊이는 적합한 샘플의 수에 따라 달라지기 때문입니다. 이러한 이유로 총 인스턴스 수도 고려한 공식이 필요합니다. 논문에서 제안한 공식은 다음과 같습니다.
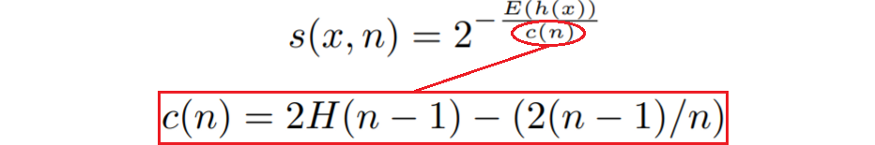
여기서 n 은 인스턴스 수, h(x) 는 데이터 포인트가 특정 트리에서 발견되는 깊이( E(h(x)) 는 여러 트리에 대한 평균), H 는 조화 번호입니다.
s(x, n) 은 0과 1 사이의 숫자로, 점수가 높을수록 이상값일 가능성이 높습니다.
참고: Scikit-learn의 구현은 위에 정의된 점수 의 반대 를 반환합니다. 따라서 위에서 말한 것은 여전히 유효하지만 음수 부호가 있습니다.
작은 데이터 세트에서 점수는 다음과 같이 제공됩니다.
scores = iforest.score_samples(df)
각 포인트에 대해 추정된 점수를 살펴보겠습니다.
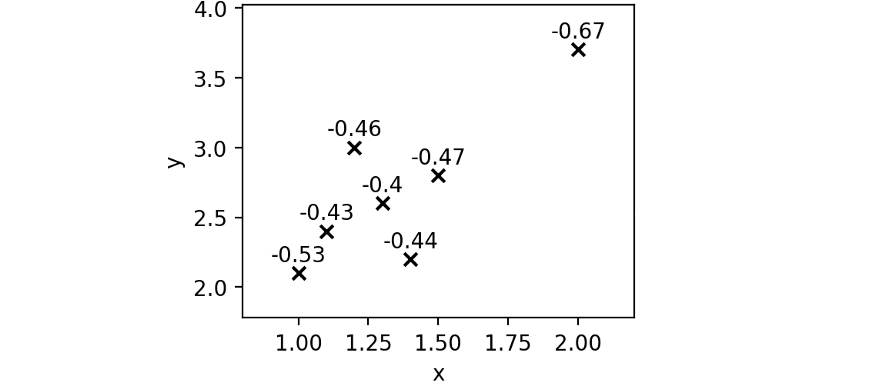
예상대로 G는 다른 모든 점수보다 점수가 낮기 때문에 이상값일 가능성이 더 큽니다.
장난감 데이터 세트 외에도 특정 경우에 알고리즘이 산출하는 결과를 시뮬레이션하는 것은 흥미로웠습니다. 예를 들어, 두 변수( x 및 y )에 대해 대략적으로 원 모양을 형성하는 일부 데이터 포인트를 취하는 경우 Isolation Forest를 통해 얻을 수 있는 점수의 등고선입니다.
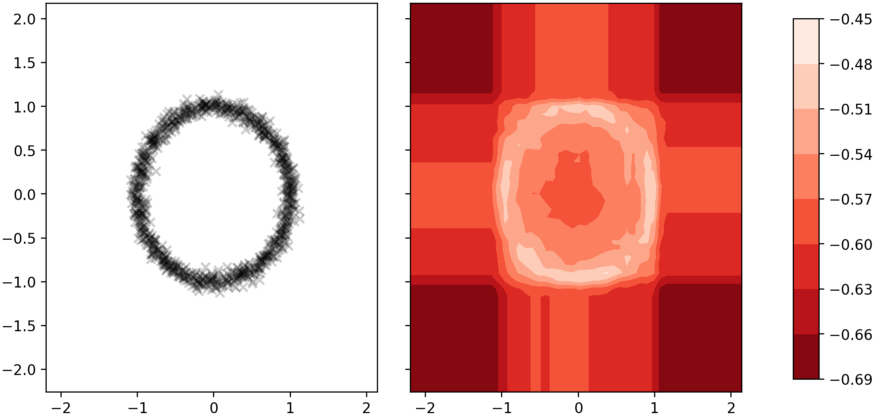
흥미롭게도 가장 극단적인 영역은 이상값일 가능성이 높을 뿐만 아니라 x 와 y 의 비정상적 조합이기 때문에 원의 중심에 있는 부분이기도 합니다 .
'Daily Review' 카테고리의 다른 글
| CRM 분석, RFM 분석 (1) | 2022.09.02 |
|---|---|
| model.fit() 데이터 사이언티스트를 위한 자리는 없습니다. (0) | 2022.09.02 |
| 데이터사이언티스트에게 필요한 3가지 이상 탐지 모델(Anomaly Detection) (0) | 2022.09.01 |
| Data-Driven Organization을 향한 디자인 씽킹 (0) | 2022.09.01 |
| LSTM AE를 활용한 이상 탐지 프로젝트 (0) | 2022.09.01 |




댓글