이름에서 알 수 있듯이 이상치는 나머지 관측치와 크게 다른 데이터 포인트입니다. 즉, 데이터의 평균 경로에서 멀리 떨어져 있습니다.
통계 및 기계 학습에서 이상값을 감지하는 것은 모델의 성능에 영향을 미칠 수 있으므로 중요한 단계입니다. 즉, 판매된 단위의 양을 기반으로 회사의 수익을 예측하려고 한다고 상상해 보십시오.
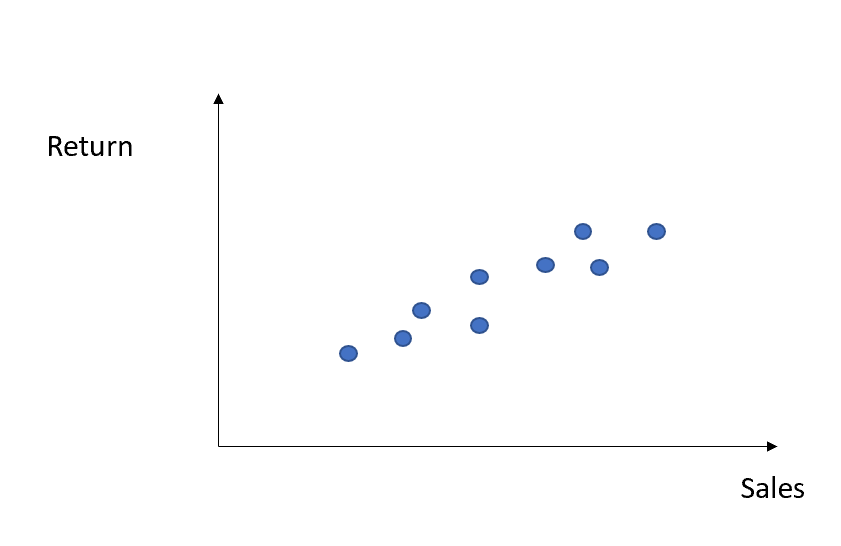
그렇게 하려면 단순 선형 회귀로 데이터를 맞추려고 하므로 OLS 전략을 진행하여 매개변수 알파 와 베타 를 찾습니다(선형 회귀에 대한 자세한 내용은 여기에서 제 이전 기사를 읽을 수 있습니다 ).
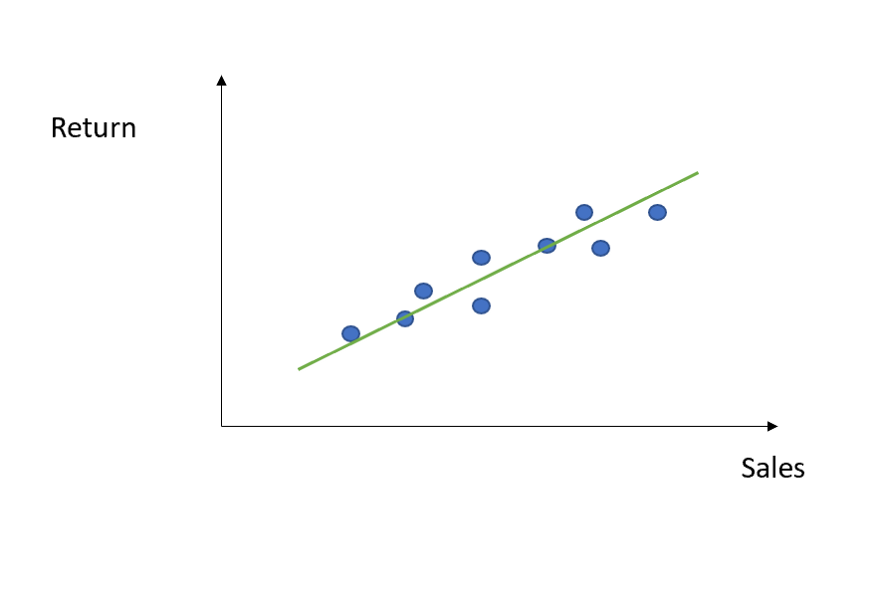
좋습니다. 하지만 데이터 중 특이치가 있다면 어떻게 될까요?
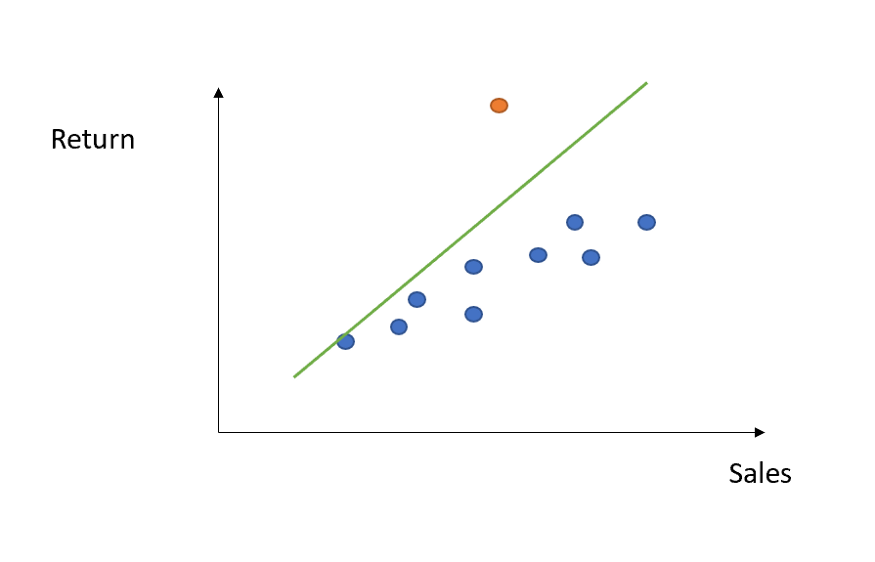
보시다시피 회귀선은 해당 이상값의 효과도 캡처하려고 하므로 더 가파르게 됩니다. 결과적으로 다른 모든 데이터 포인트를 맞추는 데 정확도가 떨어졌습니다. 가능한 해결 방법 중 하나는 모든 이상값을 감지한 후(나중에 방법을 알려줌) 단순히 제거하거나 조금 더 정교하게 해당 기능의 평균 또는 중앙값으로 대체하는 것입니다.
그러나 이 절차에는 함정이 있습니다. 실제로 이상값(적어도 전부는 아님)이 반드시 나쁜 것은 아닙니다. 실제로, 미래에 반복될 수 있는 평균 패턴과의 편차에 대한 관련 정보를 포함할 수 있습니다. 따라서 이 정보를 캡처하지 않는 모델은 예측하는 동안 이러한 편차를 방지하거나 최소한 모델링할 수 없습니다.
즉, 많은 기계로 작업하는 공장을 상상해보십시오. 이러한 후자는 시간이 지남에 따라 모니터링해야 합니다. 압력만 추적한다고 가정해 보겠습니다. 하루 중 순간과 워크플로의 양에 따라 주어진 패턴을 따를 가능성이 높습니다. 그런 다음 갑자기 압력 값의 피크를 감지하면 모든 것이 정상으로 돌아옵니다. 직관적으로, 당신은 방금 본 것을 무시할 것인가, 아니면 이 정점에 머물 것인가? 아마도 이 피크는 기술적인 문제를 예상하고 있으므로 이 정보를 통합하고 잠재적인 오류를 방지하는 데 사용하는 것이 좋습니다.
따라서 이상값 탐지에 특별한 주의를 기울여야 합니다. 특히 누락된 경우 많은 비용이 드는 결과가 발생하는 분야(사기 탐지, 사이버 보안 등을 생각해 보십시오). 그렇기 때문에 히스토그램이나 박스플롯과 같은 단순한 시각화 방법이 아닌 이상 탐지를 위한 특정 알고리즘을 사용해야 합니다.
PyOD가 도움이 되는 곳입니다.
PyOD 이상값 감지 알고리즘
PyOD는 콘솔에서 pip install pyod 를 통해 쉽게 설치할 수 있는 Python 패키지입니다 . 효율적인 방식으로 이상값을 감지하는 다양한 기능 또는 알고리즘을 제공하며, 각각은 소위 이상값을 반환합니다. 내부 임계값과 비교할 숫자로 각 데이터 포인트에 레이블을 지정하여 해당 데이터 포인트가 해당 데이터 포인트인지 여부를 결정합니다. 국외자. 그 중 몇 가지를 살펴보겠습니다.
- ABOD(Angle-based Outlier Detection): 이러한 이웃 간의 관계를 고려하지 않고 각 점과 해당 이웃 간의 관계를 고려합니다. 모든 이웃에 대한 가중 코사인 점수의 분산은 외부 점수로 볼 수 있습니다. ABOD 방법은 고차원 공간의 거리보다 각도가 더 강력한 측정값이기 때문에 고차원 데이터에 특히 유용합니다.
- K-최근접 이웃: 분류 알고리즘 KNN 뒤에 있는 수학을 사용합니다. 실제로 모든 데이터 포인트에 대해그것까지의 거리k번째가장 가까운 이웃은 외부 점수로 볼 수 있습니다.. PyOD는 k번째 이웃의 거리, k번째 이웃의 평균, k번째 이웃까지의 중앙값을 각각 외부 점수로 사용하는 최대, 평균 및 중앙값의 세 가지 KNN 감지기를 지원합니다.
- Isolation Forest: 의사결정나무와 랜덤포레스트의 이론에 따라 구축된다. 그러나 이 경우 루트는 무작위로 선택되며 이상치는 루트에 가깝게 놓여야 한다는 아이디어입니다. 정상 지점은 식별할 파티션이 많이 필요한 반면 이상치는 더 적은 파티션으로 쉽게 식별되기 때문입니다.
- LOCI(Local Correlation Integral): 이상값 및 이상값 그룹을 감지하는 데 매우 효과적입니다. 포인트 주변 영역의 데이터에 대한 많은 정보를 요약하는 각 포인트에 대한 LOCI 플롯을 제공합니다.
KNN을 위한 Python 구현을 살펴보겠습니다.
이상값 탐지를 위한 KNN
우선, KNN이 실제로 어떻게 작동하는지에 대해 매우 간략하게 요약해 보겠습니다.
KNN은 아마도 분류 작업을 위한 가장 쉬운 알고리즘일 것입니다. 유사한 관찰이 서로 가까이 있어야 한다는 것을 핵심 아이디어로 가정합니다. 구체적으로 무엇을 의미합니까? 다음과 같은 2-클래스 관찰이 있다고 상상해 보십시오.
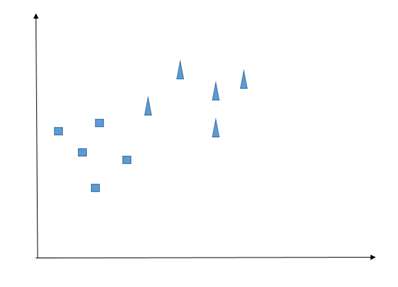
우리 수업은 정사각형과 삼각형입니다. 이제 우리는 새로운 발생(원으로 표시된 관찰)에 직면하고 이것이 삼각형인지 정사각형인지 확인하려고 합니다.

예상대로 KNN은 수학 용어로 '거리'로 번역될 수 있는 '유사성' 측면에서 이유를 설명합니다. 예를 들어, 여기에서 녹색 관찰과 일부 가장 가까운 관찰 사이의 유클리드 거리를 계산할 수 있습니다(후자의 수는 모델을 훈련하기 전에 설정해야 하는 값이며 종종 K 로 표시됨). 그런 다음 각 클래스에 대한 가장 가까운 이웃의 수를 간단히 계산합니다. 가장 높은 숫자가 새 관찰의 구성원을 결정합니다.
즉, K=3으로 설정하면 다음과 같은 문제가 발생합니다.
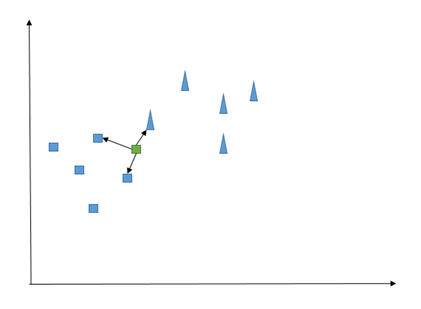
두 개의 정사각형과 하나의 삼각형을 셀 수 있으므로 새 데이터 포인트는 정사각형이어야 합니다. 좋은 경험 법칙: 반반 계산을 피할 수 있도록 K를 홀수와 동일하게 설정하십시오.
이제 파이썬으로 구현해 보자. 첫째, PyOD는 일부 이상값이 있는 임의 데이터 세트를 생성하기 위해 일부 내장 함수를 제공합니다.
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
from pyod.models.knn import KNN
from pyod.utils.data import generate_data
outlier_fraction = 0.1
n_train = 200
n_test = 100
X_train, y_train, X_test, y_test = generate_data(n_train=n_train, n_test=n_test, contamination=outlier_fraction)
#let's plot our train and test set
feature_1_train = X_train[:,[0]].reshape(-1,1)
feature_2_train = X_train[:,[1]].reshape(-1,1)
feature_1_test = X_test[:,[0]].reshape(-1,1)
feature_2_test = X_test[:,[1]].reshape(-1,1)
# scatter plot
plt.scatter(feature_1_train,feature_2_train)
plt.scatter(feature_1_test,feature_2_test)
plt.xlabel('feature_1')
plt.ylabel('feature_2')
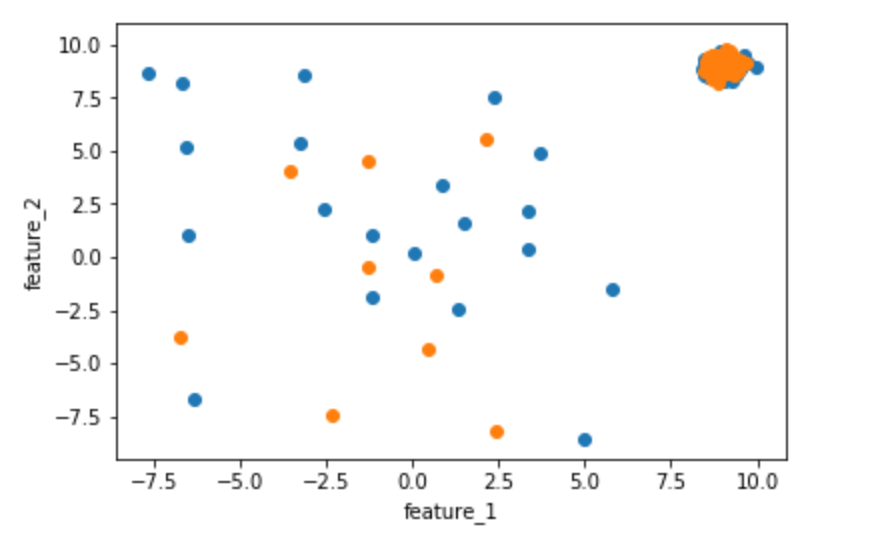
이제 KNN 모델을 사용하여 학습하고 예측해 보겠습니다.
knn=KNN(contamination=outlier_fraction)
knn.fit(X_train)
# get the prediction labels and outlier scores of the training data
y_train_pred = knn.labels_
y_train_scores = knn.decision_scores_
# get the prediction on the test data
y_test_pred = knn.predict(X_test)
y_test_scores = knn.decision_function(X_test)
# no of errors in test set
n_errors = (y_test_pred != y_test).sum()
print('No of Errors in test set: {}'.format(n_errors))
#accuracy in test set
print('Accuracy in test set: {}'.format((n_test-n_errors)/n_test))

좋습니다. 우리 알고리즘은 거의 모든 이상값을 정확하게 분류할 수 있었습니다. 피팅 절차도 시각화해 보겠습니다.
from pyod.utils import example
example.visualize(knn, X_train, y_train, X_test, y_test, y_train_pred, y_test_pred, show_figure=True, save_figure=False)
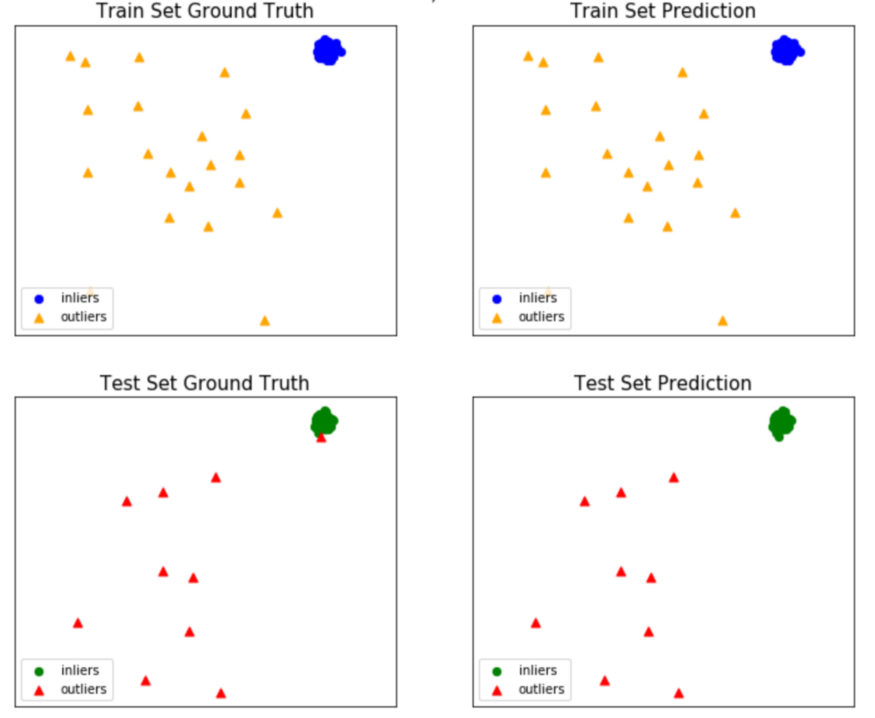
예상대로 이상값을 제대로 감지한 후에는 이를 처리하는 방법, 다시 말해 여기에 포함된 정보를 통합하는 방법을 결정해야 합니다. 이상값을 모델링하는 것은 결코 쉬운 일이 아니며 통계 및 데이터 과학의 공개 주제입니다. 예를 들어, 흥미로운 연구 분야는 극단값 이론 또는 극단값 분석(EVA)입니다. 확률 분포의 중앙값에서 극단적인 편차를 다루는 통계의 한 분야입니다. 그것은 주어진 무작위 변수의 주어진 순서 표본에서 이전에 관찰된 것보다 더 극단적인 사건의 확률을 평가하려고 합니다.
이 문서는 탐지 절차에 관한 것이므로 '모델링' 단계에 대해서는 다루지 않겠습니다. 그러나 이 주제에 관심이 있다면 다음을 추가로 읽어보기를 권합니다.
'Daily Review' 카테고리의 다른 글
| 데이터 과학자가 되어서는 안 되는 이유 (2) | 2022.09.10 |
|---|---|
| 단 6개월 만에 데이터 과학자가 되는 방법! (1) | 2022.09.09 |
| 이상 탐지를 위한 다변량 가우스 분포(Multivariate Gaussian distribution) (0) | 2022.09.09 |
| 데이터 초보자가 Excel을 즉시 배워야 하는 10가지 이유 (0) | 2022.09.08 |
| Python에서 루프와 함께 loc/iloc을 사용하지 말고 대신 이것을 사용하십시오! (0) | 2022.09.08 |




댓글