시계열 데이터 고정 검사
그럼 먼저 고정 시계열 데이터가 무엇인지 요약해 보겠습니다!
고정은 용어에서 알 수 있듯이 일관성이 있습니다. 시계열에서 계절성이나 추세가 포함되지 않은 데이터를 정상적이라고 합니다. 따라서 특정 추세 또는 계절성이 있는 다른 시계열 데이터는 고정적이지 않습니다.
우리가 작업한 두 개의 시계열 데이터 중 출산 데이터에는 추세나 계절성이 없고 고정적이라는 것을 기억할 수 있습니까? 반면, 일일 평균 기온 데이터에는 계절성 요인과 드리프트가 있으므로 비정상적이며 모델링하기 어렵습니다!
시계열의 정상성은 3가지 유형에서 두드러진다 -
(a) 고정 추세 - 이러한 종류의 시계열 데이터에는 추세가 없습니다.
(b) 계절성 고정 — 이러한 종류의 시계열 데이터에는 계절성 요인이 없습니다.
(c) Strictly Stationary — 시계열 데이터는 드리프트에 대한 변동이 거의 없이 엄격하게 일치합니다.
시계열의 정상성이 무엇인지 알았으니 어떻게 같은지 확인할 수 있습니까?
비전이 전부입니다. 현재 가지고 있는 시계열 데이터를 빠르게 시각화하면 데이터가 고정적일 수 있는지 여부를 빠르게 눈으로 검토할 수 있습니다. 다음 줄은 통계 요약입니다. 최소, 최대, 분산, 편차, 평균, 분위수 등과 같은 데이터의 요약 통계를 명확하게 살펴보면 데이터의 드리프트 또는 이동을 인식하는 데 매우 도움이 될 수 있습니다.
이것을 POC하자!
그래서 우리는 이전에 작업한 편리한 출산 데이터인 고정 데이터를 사용합니다. 그러나 비정상 데이터의 경우 단순히 월별 항공사 승객 수인 유명한 여객기 데이터를 가져와서 이들이 어떻게 고정 및 비정상인지 증명해 보겠습니다.
사례 1 - 고정 증거
import pandas as pd
import matplotlib.pyplot as plt
data = pd.read_csv('daily-total-female-births.csv', parse_dates = True, header = 0, squeeze=True)
data.hist()
plt.show()출력 -

내가 말했듯이, 비전! 시각화 자체가 가우스 분포라고 말하는 방법을 보십시오. 따라서 고정!
더 궁금하세요? 확실한 수학 증명을 하자!
X = data.values
seq = round(len(X) / 2)
x1, x2 = X[0:seq], X[seq:]
meanx1, meanx2 = x1.mean(), x2.mean()
varx1, varx2 = x1.var(), x2.var()
print('meanx1=%f, meanx2=%f' % (meanx1, meanx2)) print('variancex1=%f, variancex2=%f' % (varx1, varx2))출력 -
meanx1=39.763736, meanx2=44.185792
variancex1=49.213410, variancex2=48.708651
평균과 분산은 서로 주변에 남아 있어 데이터가 불변하므로 고정되어 있음을 분명히 보여줍니다! 엄청난.
사례 2 - 고정되지 않은 증거
import pandas as pd
import matplotlib.pyplot as plt
data = pd.read_csv('international-airline-passengers.csv', parse_dates = True, header = 0, squeeze=True)
data.hist()
plt.show()
출력 -
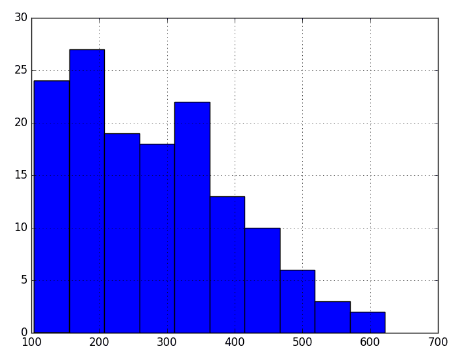
그래프는 거의 계절적인 맛을 제공합니다. 게다가 가우스 태그에 비해 너무 왜곡되어 있습니다. 이제 평균-분산 갭을 빠르게 구해 보겠습니다.
X = data.values
seq = round(len(X) / 2)
x1, x2 = X[0:seq], X[seq:]
meanx1, meanx2 = x1.mean(), x2.mean()
varx1, varx2 = x1.var(), x2.var()
print('meanx1=%f, meanx2=%f' % (meanx1, meanx2)) print('variancex1=%f, variancex2=%f' % (varx1, varx2))
출력 -
meanx1=182.902778, meanx2=377.694444
variancex1=2244.087770, variancex2=7367.962191
좋습니다. 평균과 분산 사이의 값 차이는 고정적이지 않은 종류를 선택하는 데 꽤 자명합니다
시계열 예측을 위한 ARMA, ARIMA 및 SARIMAX 모델
시계열을 예측하는 매우 전통적이지만 놀라운 '머신 러닝' 방식은 ARMA(자동 회귀 이동 평균) 및 일반적으로 ARIMA 통계 모델이라고 하는 자동 회귀 통합 이동 평균 모델입니다.
이 2가지 전통적인 접근 방식 외에도 SARIMA(계절 자동 회귀 통합 이동 평균) 및 Grid-Search ARIMA가 있습니다.
그럼, 모델들을 하나씩 살펴보도록 하겠습니다!
아르마
ARMA 모델은 AR 또는 자동 회귀 모델과 이동 평균의 2가지 통계 모델의 조합입니다.
자동 회귀 모델은 시차를 기반으로 주어진 타임스탬프 t에서 종속 변수 값 y(t)를 추정합니다. 더 나은 이해를 위해 아래 공식을 보세요.
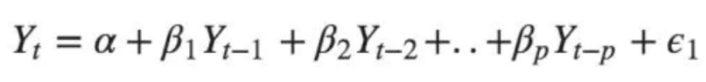
여기서 y(t) = 타임스탬프 t에서의 예측값, α = 절편 항, β = 지연 계수, y(t-1) = 타임스탬프 t-1에서의 시계열 지연.
따라서 α와 β는 y(t)를 추정하는 모델 추정기입니다.
이동 평균 모델은 유사한 역할을 하지만 이전에 롤링 평균에서 말했듯이 과거 예측 예측을 고려하지 않습니다. 오히려 아래 공식과 같이 이전에 예측된 값의 지연된 예측 오차를 사용하여 미래 값을 예측합니다.

AR 및 MA 모델이 International-Airline-Passengers 데이터에서 어떻게 수행되는지 봅시다.
AR 모델
AR_model = ARIMA(indexedDataset_logScale, order=(2,1,0))
AR_results = AR_model.fit(disp=-1)
plt.plot(datasetLogDiffShifting)
plt.plot(AR_results.fittedvalues, color='red')
plt.title('RSS: %.4f'%sum((AR_results.fittedvalues - datasetLogDiffShifting['#Passengers'])**2))

RSS 또는 잔차 제곱합은 AR 모델의 경우 1.5023이며, AR이 비정상성을 충분히 캡처하지 못하기 때문에 다소 불만족스럽습니다.
MA Model
MA_model = ARIMA(indexedDataset_logScale, order=(0,1,2))
MA_results = MA_model.fit(disp=-1)
plt.plot(datasetLogDiffShifting)
plt.plot(MA_results.fittedvalues, color='red')
plt.title('RSS: %.4f'%sum((MA_results.fittedvalues - datasetLogDiffShifting['#Passengers'])**2))

MA 모델은 AR과 유사한 결과를 보이지만 매우 작은 차이가 있습니다. 데이터가 고정적이지 않다는 것을 알고 있으므로 비정상 처리기 AR+I+MA를 사용하여 이 RSS 점수를 개선합시다!
ARIMA
이전에 사용된 AR 및 MA 모델의 축소된 사용과 함께 ARIMA는 더 나은 예측을 위해 고정되지 않은 데이터를 고정적으로 만들기 위해 일부 관측치를 차별화할 목적으로 통합(I)의 특수 개념을 사용합니다. 따라서 고정 데이터만 처리할 수 있었던 이전 ARMA보다 확실히 낫습니다.

차분 요소가 하는 일은 두 타임스탬프(예: t 및 t+1) 간의 예측 값 차이를 고려한다는 것입니다. 이렇게 하면 변동이 심한 '비정상' 평균보다 일정한 평균을 얻는 데 도움이 됩니다.
ARIMA로 동일한 데이터를 피팅하고 얼마나 잘 수행되는지 봅시다!
ARIMA_model = ARIMA(indexedDataset_logScale, order=(2,1,2))
ARIMA_results = ARIMA_model.fit(disp=-1)
plt.plot(datasetLogDiffShifting)
plt.plot(ARIMA_results.fittedvalues, color='red')
plt.title('RSS: %.4f'%sum((ARIMA_results.fittedvalues - datasetLogDiffShifting['#Passengers'])**2))

엄청난! 그래프 자체는 ARIMA가 ARMA와 비교하여 어떻게 우리 데이터를 잘 일반화된 방식으로 맞추는지 알려줍니다! 또한 RSS가 1.5023 또는 1.4721에서 1.0292로 어떻게 떨어졌는지 관찰하십시오.
SARIMAX
ARIMA, SARIMAX 또는 외생 요인이 있는 계절적 자동 회귀 통합 이동 평균에 대한 멋진 확장으로 설계 및 개발되었으며 계절성 이 높은 시계열의 경우 ARIMA보다 더 나은 플레이어입니다. SARIMAX가 고려하는 4가지 계절 구성 요소가 있습니다.
그들은 -
1. 계절적 자기회귀 성분
2. 계절 이동 평균 구성 요소
3. 계절적 무결성 주문 구성 요소
4. 계절적 주기성

당신이 저처럼 이론에 민감한 사람이라면 여기 에서 더 많은 정보를 읽으십시오. 공식의 세부 사항에 들어가는 것은 이 기사의 범위를 벗어납니다!
이제 SARIMAX가 International-Airline-Passengers 데이터와 같은 계절별 시계열 데이터에 대해 얼마나 잘 수행하는지 봅시다.
from statsmodels.tsa.statespace.sarimax import SARIMAX
SARIMAX_model=SARIMAX(train['#Passengers'],order=(1,1,1),seasonal_order=(1,0,0,12))
SARIMAX_results=SARIMAX_model.fit()
preds=SARIMAX_results.predict(start,end,typ='levels').rename('SARIMAX Predictions')
test['#Passengers'].plot(legend=True,figsize=(8,5))
preds.plot(legend=True)
SARIMAX가 계절 시계열을 얼마나 아름답게 처리하는지 보십시오!

복잡한 시계열 예측을 위한 DL 방법으로 이동
시계열 데이터의 매우 일반적인 기능 중 하나는 장기 종속성 요인입니다. 많은 시계열 예측이 이전 기록에서 작동한다는 것은 분명합니다(미래는 이전 기록을 기반으로 예측되며 훨씬 뒤쳐질 수 있음). 따라서 ARIMA, ARMA 또는 SARIMAX와 같은 일반적인 기존 기계 학습 모델은 장기 종속성을 캡처할 수 없으므로 시퀀스 종속 시계열 문제에서 열등한 사람이 됩니다.

순환 신경망
이러한 문제를 해결하기 위해 시퀀스 종속성을 비정상적으로 처리할 수 있는 매우 지능적이고 강력한 신경망 아키텍처가 제안되었습니다. 순환 신경망 또는 RNN으로 알려져 있습니다.
RNN은 시계열과 같은 순차적 데이터에서 작동하도록 설계되었습니다. 그러나 RNN의 매우 주목할 만한 함정은 장기적인 종속성을 처리할 수 없다는 것입니다. 엄청난 수의 이전 레코드를 기반으로 시계열을 예측하려는 문제의 경우 RNN은 훨씬 이전에 발생한 이전 레코드의 최대값을 잊어버리고 신경망에 제공된 최근 데이터 시퀀스만 학습합니다. 따라서 RNN은 NLP 및 시계열에서 NSP(Next Sequence Prediction) 작업에 대한 표시에 미치지 못하는 것으로 관찰되었습니다.
장기 종속성을 포착하지 못하는 이 문제를 해결하기 위해 LSTM(Long Short Term Memory) 네트워크라고 하는 강력한 RNN 변형이 개발되었습니다. 단기 시퀀스/종속성만 캡처할 수 있는 RNN과 달리 LSTM은 이름에서 알 수 있듯이 단기 종속성뿐만 아니라 장기 학습도 관찰되었습니다. 따라서 시계열 데이터를 모델링하고 예측하는 데 큰 성공을 거두었습니다!
참고 — LSTM의 아키텍처를 설명하는 것은 이 블로그의 크기를 넘어서므로 LSTM에 대해 자세히 설명한 제 기사 로 이동하는 것이 좋습니다!
이제 항공사 승객의 데이터를 가져와서 RNN과 LSTM이 얼마나 잘 작동하는지 봅시다!
수입품 -
import numpy as np
import pandas as pd
import tensorflow as tf
import matplotlib.pyplot as plt
import sklearn.preprocessing
from sklearn.metrics import r2_score
from keras.layers import Dense, Dropout, SimpleRNN, LSTM
from keras.models import Sequential
더 나은 예측을 위해 데이터를 안정적으로 조정하기 -
minmax_scaler = sklearn.preprocessing.MinMaxScaler()
data['Passengers'] = minmax_scaler.fit_transform(data['Passengers'].values.reshape(-1,1))
data.head()
확장된 데이터 샘플-

훈련, 테스트 분할(80–20 비율) -
split = int(len(data[‘Passengers’])*0.8)
x_train,y_train,x_test,y_test = np.array(x[:split]),np.array(y[:split]),
np.array(x[split:]), np.array(y[split:])
#reshaping data to original shape
x_train = np.reshape(x_train, (split, 20, 1))
x_test = np.reshape(x_test, (x_test.shape[0], 20, 1))
RNN 모델 -
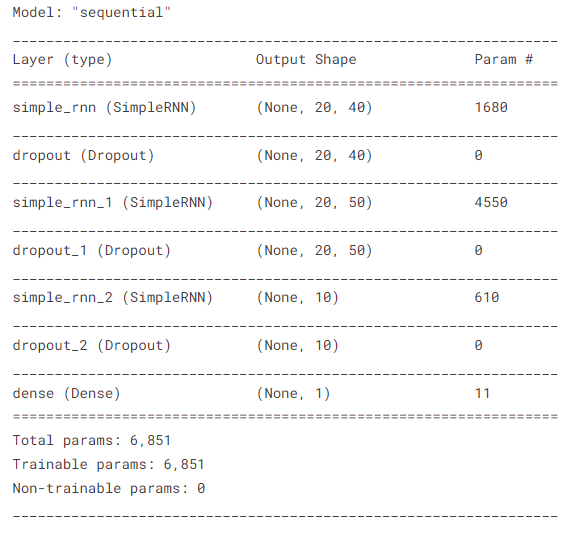
model = Sequential()
model.add(SimpleRNN(40, activation="tanh", return_sequences=True, input_shape=(x_train.shape[1],1)))
model.add(Dropout(0.15))
model.add(SimpleRNN(50, return_sequences=True, activation="tanh"))
model.add(Dropout(0.1)) #remove overfitting
model.add(SimpleRNN(10, activation="tanh"))
model.add(Dense(1))
model.summary()
컴파일, 피팅 및 예측-
model.compile(optimizer="adam", loss="MSE")
model.fit(x_train, y_train, epochs=15, batch_size=50)
preds = model.predict(x_test)

모델이 얼마나 잘 예측하는지 그림을 보여드리겠습니다.

꽤 정확합니다!
LSTM 모델 -
model = Sequential()
model.add(LSTM(100, activation="ReLU", return_sequences=True, input_shape=(x_train.shape[1], 1)))
model.add(Dropout(0.2))
model.add(LSTM(80, activation="ReLU", return_sequences=True))
model.add(Dropout(0.2))
model.add(LSTM(50, activation="ReLU", return_sequences=True))
model.add(Dropout(0.2))
model.add(LSTM(30, activation="ReLU"))
model.add(Dense(1))
model.summary()

컴파일, 피팅 및 예측-
model.compile(optimizer="adam", loss="MSE")
model.fit(x_train, y_train, epochs=15, batch_size=50)
preds = model.predict(x_test)모델이 얼마나 잘 예측하는지 사진으로 보여드리겠습니다.

여기서 우리는 RNN이 LSTM보다 작업을 더 잘 수행한다는 것을 쉽게 관찰할 수 있습니다. 분명히 알 수 있듯이 LSTM은 훈련 데이터에서는 훌륭하게 작동하지만 무효화/테스트 데이터는 좋지 않아 과적합의 징후를 보여줍니다!
따라서 장기 종속성 학습이 필요한 경우에만 LSTM을 사용하십시오. 그렇지 않으면 RNN이 충분히 잘 작동합니다.
'Daily Review' 카테고리의 다른 글
| 머신 러닝 인터뷰 준비 팁 (0) | 2022.09.13 |
|---|---|
| Matplotlib 차트를 향상시키는 7가지 간단한 방법 (0) | 2022.09.12 |
| 시계열 분석 및 예측에 대한 종합 가이드 (2) (0) | 2022.09.12 |
| 시계열 분석 및 예측에 대한 종합 가이드 (1) (0) | 2022.09.11 |
| 올바른 데이터에 대한 올바른 차트 (0) | 2022.09.11 |




댓글