시계열 성분 조합론
시계열 모델은 2가지 방법론으로 나타낼 수 있습니다.
가법 방법론 -
시계열 추세가 적분 간의 선형 관계인 경우, 즉 계열의 주파수(너비)와 진폭(높이)이 같으면 가법 규칙이 적용됩니다.
덧셈 방법론은 계절적 변동이 타임스탬프에 대해 선형이거나 일정한 시계열이 있을 때 사용됩니다.
다음과 같이 나타낼 수 있습니다.
y(t) 또는 x(t) = 수준 + 추세 + 계절성 + 노이즈
여기서 모델 y(다변량) 또는 x(단변량)은 시간 t의 함수입니다.
승법 방법론 -
시계열이 적분 사이의 선형 관계가 아닌 경우 곱셈 규칙에 따라 모델링이 수행됩니다.
승법 방법론은 계절적 변동이 시간에 따라 증가하는 시계열이 있을 때 사용되며, 이는 지수 또는 2차일 수 있습니다.
그것은 다음과 같이 표현됩니다-
y(t) 또는 x(t)= 수준 * 추세 * 계절성 * 노이즈
지도 시계열 예측에 대해 자세히 알아보기
지도 학습은 가장 많이 사용되는 도메인별 기계 학습이므로 지도 시계열 예측에 중점을 둡니다.
여기에는 마지막에 독자가 다음 방법을 알 수 있도록 다양한 세부 주제가 포함됩니다.
- 시계열 데이터를 로드하고 기술 통계를 사용하여 탐색
- 추가 모델링을 위해 시계열 데이터 확장 및 정규화
- 시계열 데이터에서 유용한 기능 추출(Feature Engineering)
- 시계열의 정상성을 확인하여 줄이기
- 시계열 예측을 위한 ARIMA 및 그리드 검색 ARIMA 모델
- 더 복잡한 시계열 예측(LSTM 및 bi-LSTM)을 위한 딥 러닝 방법으로 이동
그래서 더 이상 고민하지 않고 시작하겠습니다!
시계열 데이터를 로드하고 기술 통계를 사용하여 탐색
시계열 데이터의 쉽고 빠른 이해와 분석을 위해 'Daily Female Births Dataset'이라는 유명한 장난감 데이터 세트에 대해 작업합니다.
여기 에서 데이터세트를 다운로드 하세요 .
필요한 라이브러리 가져오기 및 데이터 로드 -
import numpy import pandas
import statmodels import matplotlib.pyplot as plt
import seaborn as sns
data = pd.read_csv('daily-total-female-births-in-cal.csv', parse_dates = True, header = 0, squeeze=True)
data.head()이것은 우리가 얻는 출력입니다-
1959-01-01 35 1959-01-02 32 1959-01-03 30 1959-01-04 31 1959-01-05 44
Name: Daily total female births in California, 1959, dtype: int64참고 — 날짜를 구문 분석할 수 있는 datetime 개체로 변환하기 때문에 'parse_dates'를 사용해야 하며, 쉽게 참조할 수 있도록 명명된 열이 저장되도록 하는 header=0, 단일 개체의 데이터 프레임을 변환하는 squeeze=True를 사용해야 합니다. 요소를 스칼라로 변환합니다.
시계열 데이터 탐색 -
print(data.size) #output-365
(a) 몇 가지 기술 통계를 수행하십시오.
print(data.describe())
출력 -
count 365.000000 mean 41.980822 std 7.348257 min 23.000000 25% 37.000000 50% 42.000000 75% 46.000000 max 73.000000
(b) 시계열 분포도 살펴보기 -
pyplot.plot(series) pyplot.show()

추가 모델링을 위해 시계열 데이터 확장 및 정규화
정규화된 데이터는 경사 하강법 및 손실 최적화가 빠르고 효율적이며 로컬 최소값으로 빠르게 수렴하도록 훈련 데이터의 숫자 기능을 0과 1 범위로 확장합니다. 기능 스케일링(feature scaling)으로 상호 교환 가능하게 알려진 이는 모든 ML 문제 설명에 중요합니다.
시계열 데이터에서 정규화를 달성하는 방법을 살펴보겠습니다.
이를 위해 변동이 심한 시계열 데이터인 최소 일일 온도 데이터를 선택하겠습니다. 여기 잡아 !
데이터의 극도로 변동하는 특성을 살펴보겠습니다.
강한 계절적 적분을 가지고 있음을 알 수 있다. 따라서 스케일링은 계절적 적분을 제거하는 데 중요하며, 이는 독립 피쳐와 대상 피쳐 간의 명확한 관계 설정으로 이어집니다!
기능을 정규화하려면 Scikit-learn의 MinMaxScaler가 너무 편리합니다! 예측 후 원본 데이터 포인트를 생성하려면 이 멋진 내장 함수에서 inverse_transform() 함수도 제공합니다!
다음은 정규화 코드입니다.
# import necessary libraries
import pandas
from sklearn.preprocessing import MinMaxScaler
# load and sanity check the data
data = read_csv('daily-minimum-temperatures-in-me.csv',
parse_dates = True,
header = 0,
squeeze=True,
index_col=0)
print(data.head())
#convert data into matrix of row-col vectors values = data.values values = values.reshape((len(values), 1))
# feature scaling
scaler = MinMaxScaler(feature_range=(0, 1))
#fit the scaler with the train data to get min-max values
scaler = scalar.fit(values)
print('Min: %f, Max: %f' % (scaler.data_min_, scaler.data_max_))
# normalize the data and sanity check
normalized = scaler.transform(values)
for i in range(5):
print(normalized[i])
# inverse transform to obtain original values
original_matrix= scaler.inverse_transform(normalized)
for i in range(5):
print(original_matrix[i])
우리가 무엇을 얻었는지 살펴 봅시다 -
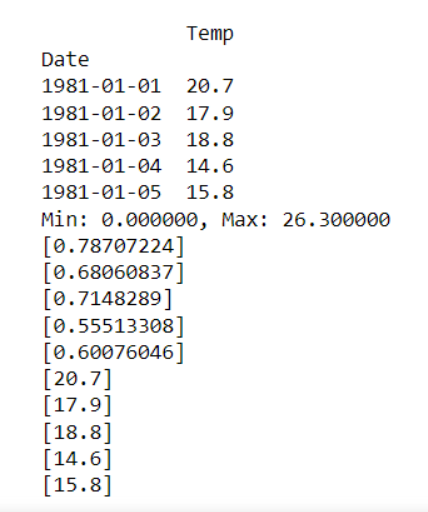
값이 어떻게 조정되었는지 확인하십시오!
참고 — 우리의 경우 데이터에 이상값이 없으므로 MinMaxScaler가 목적을 잘 해결합니다. 비지도 학습 접근 방식이 있고 데이터에 이상치가 포함되어 있는 경우 정규화를 통해 데이터를 평균에 가깝게 확장하기 때문에 정규화보다 더 강력한 표준화를 선택하는 것이 좋습니다. 가난한 모델에게. 반면에 표준화는 표준 편차 값이 1이고 평균이 0인 큰 간격을 사용하므로 이상값 처리가 강력합니다.
자세한 내용은 여기 !
시계열 데이터에서 유용한 기능 추출(기능 엔지니어링)
데이터를 지도 학습 문제로 프레이밍하는 것은 유용한 기능을 처리 및 추출하고 관련 없는 기능을 삭제하여 모델을 강력하고 비용 효율적으로 만드는 작업을 간단하게 처리합니다.
지도 학습 문제에는 독립(x)과 종속/목표(y)의 두 가지 유형의 기능이 있다는 것을 이미 알고 있습니다. 따라서 목표 값을 얼마나 더 잘 달성하느냐는 우리가 독립 기능을 얼마나 잘 선택하고 엔지니어링하느냐에 달려 있습니다.
이제 시계열 데이터에는 두 개의 열, 타임스탬프 및 해당 값이 있다는 것을 알아야 합니다. 따라서 시계열 문제에서 독립 특성이 시간이고 종속 특성이 값이라는 것은 매우 자명합니다.
이제 이 두 변수 간의 고유한 관계가 설정되어 가능한 한 좋은 예측을 할 수 있도록 이러한 입력 및 출력 값으로 설계해야 하는 기능이 무엇인지 살펴보겠습니다.
시계열에서 입력 및 출력 변수 간의 관계를 모델링하는 데 매우 중요한 기능은 다음과 같습니다.
1. 기술적인 통계적 특징 — 들리는 것처럼 매우 간단하지만 모든 데이터의 통계적 세부사항과 요약을 계산하는 것은 매우 중요합니다. 평균, 중앙값, 표준 편차, 분위수 및 최소값-최대값. 이는 이상값 감지, 크기 조정 및 정규화, 분포 인식 등과 같은 작업에서 매우 편리합니다.
2. 창 통계 기능 - 창 기능은 이전 타임스탬프의 고정 창 크기에 대한 다양한 통계 작업의 통계 요약입니다. 일반적으로 창에서 기술 통계를 추출하는 두 가지 방법이 있습니다. 그들은
(a) 롤링 윈도우 통계 : 롤링 윈도우는 롤링 평균 또는 우리가 일반적으로 이동 평균이라고 부르는 것과 종종 기타 통계 연산을 계산하는 데 중점을 둡니다. 이것은 특정 슬라이딩 윈도우 내의 값에 대한 요약 통계(대부분 평균)를 계산한 다음 이를 데이터 세트의 기능으로 할당할 수 있습니다.
타임스탬프 t-1의 평균은 x이고 t-2는 y이므로 x와 y의 평균을 찾아 타임스탬프 t+1의 값을 예측합니다. 따라서 롤링 윈도우는 세 번째 값을 예측하기 위해 2개의 값의 평균을 취합니다. 이 작업이 완료되면 창은 다음 값 집합으로 이동하므로 2개의 값으로 구성된 각 창에 대해 평균이 계산됩니다. 예측에는 이전 데이터가 아니라 최근 데이터가 더 중요할 때 롤링 윈도우 통계를 더 자주 사용합니다.
롤링 윈도우를 사용하여 이동 평균 또는 롤링 평균을 계산하는 방법을 살펴보겠습니다.
from pandas import DataFrame
from pandas import concat
df = DataFrame(data.values)
tshifts = df.shift(1)
rwin = tshifts.rolling(window=2)
moving_avg = rwin.mean()
joined_df = concat([moving_avg, df], axis=1)
joined_df.columns = ['mean(t-2,t-1)', 't+1'] print(joined_df.head(5))
우리가 무엇을 얻었는지 살펴 봅시다 -
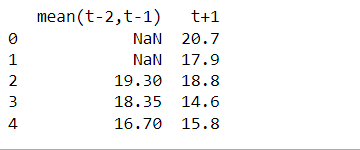
(b) 확장 창 통계 : 롤링 창과 거의 유사하게 확장 창은 확장할 때마다 예측 값과 이전 관측값을 모두 추출하는 추가 습관을 고려합니다. 이는 이전 데이터가 최근 데이터와 마찬가지로 예측에 똑같이 중요할 때 유용합니다.
확장 창 코드에 대해 간단히 살펴보겠습니다.
window = tshifts.expanding()
joined_df2 = concat([rwin.mean(),df.shift(-1)], axis=1)
joined_df2.columns = ['mean', 't+1']
print(joined_df2.head(5))
우리가 무엇을 얻었는지 살펴 봅시다 -
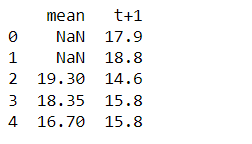
3. 지연 기능 — 지연은 단순히 이전 타임스탬프(예: t-1)의 값을 알고 있는 경우 타임스탬프 t+1의 값을 예측하는 것입니다. 단순히 2개의 다른 타임스탬프에서 두 값 사이의 거리 또는 지연입니다.
4. 날짜/시간 기능 — 더 나은 예측을 위해 온도 값과 함께 월 또는 일과 같은 특정 구성 요소로 시간을 변환하는 것입니다. 이렇게 하면 각 레코드의 특정 타임스탬프에서 월과 일에 대한 특정 정보를 수집할 수 있습니다.
5. 타임스탬프 분해 - 타임스탬프 분해에는 고유하고 특별한 타임스탬프를 저장하기 위해 타임스탬프를 타임스탬프의 하위 집합 열로 나누는 작업이 포함됩니다. 디왈리 또는 크리스마스, 즉 크래커와 산타 모자 판매가 시작되기 전에 과일 케이크는 연중 다른 시기보다 기하급수적으로 증가합니다. 따라서 원본 타임스탬프를 하위 집합으로 분해하여 이러한 특수 타임스탬프를 저장하는 것은 예측에 유용합니다.
'Daily Review' 카테고리의 다른 글
| Matplotlib 차트를 향상시키는 7가지 간단한 방법 (0) | 2022.09.12 |
|---|---|
| 시계열 분석 및 예측에 대한 종합 가이드 (3) (0) | 2022.09.12 |
| 시계열 분석 및 예측에 대한 종합 가이드 (1) (0) | 2022.09.11 |
| 올바른 데이터에 대한 올바른 차트 (0) | 2022.09.11 |
| SQL에서 하기 가장 어려운 5가지 (1) | 2022.09.11 |




댓글