Intro
클러스터링은 알고리즘이 "실제" 레이블 없이 유사한 데이터 포인트를 그룹화하는 비지도 학습 작업입니다. 데이터 포인트 간의 유사성은 일반적으로 유클리드 거리( Euclidean distance )라고 하는 거리 측정법으로 측정됩니다 .
서로 다른 시계열을 유사한 그룹으로 클러스터링하는 것은 각 데이터 포인트가 순서가 지정된 시퀀스이기 때문에 어려운 클러스터링 작업입니다.
시계열 클러스터링에 대한 가장 일반적인 접근 방식은 시계열을 각 시간 인덱스(또는 시리즈 집계)에 대한 열이 있는 테이블로 평면화하고 k-means 와 같은 표준 클러스터링 알고리즘을 직접 적용하는 것 입니다. (K-평균은 샘플을 k 그룹으로 분할하고 각 클러스터의 제곱합을 최소화하여 데이터 클러스터를 구성하는 일반적인 클러스터링 알고리즘입니다.)
아래 그림과 같이 이것이 항상 잘 작동하는 것은 아닙니다. 차트의 각 부분 그림은 유클리드 거리를 사용하여 k-평균 군집화에 의해 생성된 군집을 표시합니다. 빨간색의 군집 중심은 계열의 모양을 캡처하지 않습니다.

직관적으로 유클리드 거리와 같은 표준 클러스터링 알고리즘에 사용되는 거리 측정은 시계열에 적합하지 않은 경우가 많습니다. 더 나은 접근 방식은 기본 거리 측정을 동적 시간 왜곡 과 같은 시계열 비교를 위한 메트릭으로 바꾸는 것 입니다.
이 기사에서는 적응하는 방법에 대해 설명합니다.k-평균 클러스터링 동적 시간 왜곡을 사용하여 시계열로, 쉬운 코드 예제를 제공할 것입니다.
시계열에 대한 동적 시간 왜곡 거리 측정법
그러나 먼저 일반적인 유클리드 거리 측정법이 시계열 에 적합하지 않은 이유는 무엇입니까? 요컨대, 데이터의 시간 차원을 무시하고 시간 이동에 불변합니다. 두 시계열이 높은 상관 관계가 있지만 하나가 한 시간 단계만큼 이동하는 경우 유클리드 거리는 더 멀리 떨어져 있는 것으로 잘못 측정합니다. 자세한 예를 보려면 여기 를 클릭 하십시오.
대신 DTW(동적 시간 왜곡)를 사용하여 계열을 비교하는 것이 좋습니다. DTW는 시간, 속도 또는 길이가 정확히 일치하지 않는 두 시간 시퀀스 간의 유사성을 측정하는 기술입니다.
DTW 설명
계열 X =(x₀, …, xₙ) 및 계열 Y =(y₀, …, yₘ)가 주어지면 X 에서 Y 까지의 DTW 거리는 다음 최적화 문제로 공식화됩니다.

DTW 방정식을 요약하면 다음과 같습니다. DTW는 X 의 각 요소와 Y 의 가장 가까운 점 사이의 거리 제곱합의 제곱근으로 계산됩니다 . DTW(X, Y) ≠ DTW(Y, X)입니다.
이것을 더 세분화해 보겠습니다.
DTW는 시리즈 X 의 각 요소를 시리즈 Y 의 각 요소와 비교합니다(nxm 비교). 비교 d(xᵢ, yⱼ) 는 단순한 빼기 xᵢ — yⱼ 입니다.
그런 다음 X 의 각 xᵢ 에 대해 DTW는 거리 계산을 위해 Y에서 가장 가까운 점을 선택합니다.

위: DTW가 파란색 계열의 각 지점을 빨간색 계열의 가장 가까운 지점과 일치시키는 방법을 보여주는 그림. 아래: 유클리드 거리 메트릭이 두 시계열의 포인트와 어떻게 일치하는지 보여주는 그림. 시리즈의 길이가 다릅니다. 유클리드 매칭과 달리 DTW는 파란색 시리즈의 각 포인트를 빨간색 시리즈의 포인트와 비교할 수 있습니다. 출처: 위키커먼즈
이렇게 하면 X의 각 지점을 Y의 가장 가까운 지점에 정렬하는 X 와 Y 사이에 뒤틀린 "경로"가 생성 됩니다. 경로는 정렬된 계열 간의 유클리드 거리를 최소화하는 시계열의 시간적 정렬입니다.
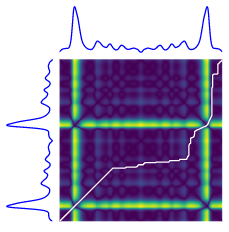
두 시계열(파란색) 사이의 DTW 경로(흰색 선)의 시각적 개체입니다. 히트 플롯은 거리 값( xᵢ — yⱼ)²을 강조 표시합니다. 출처 : tslearn 문서
동적 시간 왜곡은 복잡성이 O(MN)인 동적 프로그래밍을 사용하여 계산됩니다. 특정 알고리즘에 대한 자세한 내용을 보려면 여기 또는 여기 를 클릭 하십시오.
파이썬에서 DTW와 두 시계열을 비교하는 것은 쉽습니다.
from tslearn.metrics import dtw
dtw_score = dtw(x, y)DTW의 변형: soft-DTW
soft-DTWmin 는 미분할 수 없는 연산을 미분 가능한 연산으로 대체하는 DTW의 미분 가능한 변형입니다 (soft-min)

함수에 따라 soft-DTW 는 결과 메트릭의 평활화를 제어 하는 하이퍼 매개변수 γ 에 따라 달라집니다. DTW와 마찬가지로 soft-DTW는 동적 계획법을 사용하여 2차 시간으로 계산할 수 있습니다.
각주: soft-DTW의 주요 이점은 어디에서나 미분할 수 있다는 사실에서 비롯됩니다. 이를 통해 soft-DTW는 실제 시리즈와 예측된 시리즈를 비교하여 신경망 손실 함수로 사용할 수 있습니다.
from tslearn.metrics import soft_dtw
soft_dtw_score = soft_dtw(x, y, gamma=.1)동적 시간 왜곡을 사용한 K-평균 클러스터링
k-means 클러스터링 알고리즘은 다음과 같이 수정하면 동적 시간 왜곡이 있는 시계열에 적용할 수 있습니다.
- DTW(Dynamic Time Warping)는 유사한 모양의 시계열을 수집하는 데 사용됩니다.
- 군집 중심 또는 barycenters 는 DTW를 기준으로 계산됩니다. 무게중심 은 DTW 공간에서 시계열 그룹의 평균 시퀀스입니다 . DTW DBA ( Barycenter Averaging) 알고리즘은 군집에서 중심과 계열 간의 제곱 DTW 거리의 합을 최소화합니다. soft-DTW 알고리즘 은 군집의 중심과 계열 사이의 soft-DTW 거리의 가중치 합을 최소화합니다. 가중치는 조정할 수 있지만 합계는 1이어야 합니다.
결과적으로 중심은 구성원 사이에서 시간적 이동이 발생하는 위치에 관계없이 클러스터 구성원의 모양을 모방하는 평균 모양을 갖습니다.

맨 위 행: DTW(DBA 알고리즘)를 사용한 K-평균 클러스터링. 맨 아래 행: K-soft-DTW를 사용한 클러스터링을 의미합니다. 각 열은 서로 다른 클러스터와 해당 중심의 계열을 빨간색으로 표시합니다. 소스 + 코드 .
Python 패키지를 사용하여 tslearnk-means 및 DTW 단순으로 시계열 데이터 세트를 클러스터링:
from tslearn.clustering import TimeSeriesKMeans
model = TimeSeriesKMeans(n_clusters=3, metric="dtw", max_iter=10)
model.fit(data)
DTW 대신 soft-DTW를 사용하려면 간단히 metric="softdtw". 단일 시계열은 2차원 배열로 형식화될 것으로 예상합니다.
시계열 집합은 모양이 3차원 배열로 형식화되어야 합니다 (num_series, max_length, 1). 집합의 계열이 길이가 같지 않으면 더 짧은 계열이 NaN 값으로 증가됩니다. tslearn은 데이터 형식을 적절하게 지정 하고 다른 시계열 패키지 및 데이터 형식과 쉽게 통합 하기 위한 사용하기 쉬운 유틸리티 기능 을 제공 합니다.
'Daily Review' 카테고리의 다른 글
| An End-to-End Unsupervised Anomaly Detection (0) | 2022.08.30 |
|---|---|
| SQL을 사용한 레스토랑 판매의 탐색적 데이터 분석(EDA) (3) | 2022.08.30 |
| 머신 러닝을 위한 데이터 전처리 (0) | 2022.08.30 |
| 데이터 분석가로서 알아야 할 7가지 SQL 쿼리 (0) | 2022.08.29 |
| 최신 데이터 파이프라인을 구축하는 방법 (0) | 2022.08.29 |




댓글